Ketahui Rahasia Luas Permukaan Tabung yang Jarang Diketahui

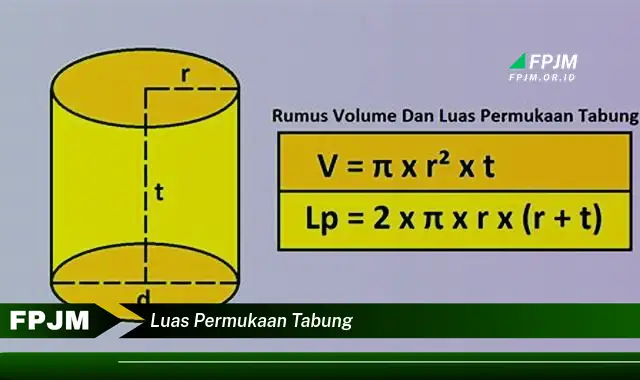
Luas permukaan tabung adalah besaran yang menyatakan ukuran seluruh permukaan tabung. Luas permukaan tabung terdiri dari luas selimut tabung dan dua kali luas alas tabung. Luas selimut tabung dihitung dengan rumus 2r(r+t), sedangkan luas alas tabung dihitung dengan rumus r. Sehingga, luas permukaan tabung dapat dihitung dengan rumus 2r(r+t) + 2r = 2r(2r+t).

Luas permukaan tabung sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran. Dalam teknik, luas permukaan tabung digunakan untuk menghitung luas permukaan pipa, tangki, dan boiler. Dalam arsitektur, luas permukaan tabung digunakan untuk menghitung luas permukaan kubah dan menara. Dalam kedokteran, luas permukaan tabung digunakan untuk menghitung luas permukaan paru-paru dan pembuluh darah.

Daftar isi

Konsep luas permukaan tabung telah dikenal sejak zaman dahulu. Ahli matematika Yunani, Archimedes, adalah orang pertama yang menghitung luas permukaan tabung pada abad ke-3 SM. Rumus yang digunakan oleh Archimedes masih digunakan hingga saat ini.

Luas Permukaan Tabung

Luas permukaan tabung merupakan besaran yang penting dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran. Luas permukaan tabung dipengaruhi oleh beberapa faktor, antara lain:

Jari-jari alas tabung (r)
Tinggi tabung (t)
Luas selimut tabung (Ls)
Luas alas tabung (La)
Rumus luas permukaan tabung (L = 2r(r+t) + 2r)
Aplikasi luas permukaan tabung
Sejarah luas permukaan tabung

Ketujuh aspek tersebut saling berkaitan dan membentuk konsep luas permukaan tabung secara keseluruhan. Misalnya, jari-jari alas tabung dan tinggi tabung menentukan luas selimut tabung dan luas alas tabung, yang pada akhirnya menentukan luas permukaan tabung. Rumus luas permukaan tabung digunakan untuk menghitung luas permukaan tabung berdasarkan jari-jari alas tabung dan tinggi tabung. Aplikasi luas permukaan tabung sangat luas, mulai dari teknik hingga kedokteran. Sejarah luas permukaan tabung menunjukkan perkembangan konsep ini dari zaman dahulu hingga sekarang.

Jari-jari alas tabung (r)

Jari-jari alas tabung (r) merupakan salah satu faktor yang menentukan luas permukaan tabung. Semakin besar jari-jari alas tabung, semakin besar pula luas permukaan tabung. Hal ini karena jari-jari alas tabung menentukan luas selimut tabung, yang merupakan bagian terbesar dari luas permukaan tabung.

Luas selimut tabung
Luas selimut tabung dihitung dengan rumus 2r(r+t), dimana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Semakin besar jari-jari alas tabung, semakin besar pula luas selimut tabung.
Luas alas tabung
Luas alas tabung dihitung dengan rumus r², dimana r adalah jari-jari alas tabung. Semakin besar jari-jari alas tabung, semakin besar pula luas alas tabung.
Luas permukaan tabung
Luas permukaan tabung dihitung dengan rumus 2r(r+t) + 2r², dimana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Semakin besar jari-jari alas tabung, semakin besar pula luas permukaan tabung.

Contohnya, sebuah tabung dengan jari-jari alas 10 cm dan tinggi 20 cm memiliki luas selimut tabung sebesar 628,32 cm², luas alas tabung sebesar 314,16 cm², dan luas permukaan tabung sebesar 1256,64 cm². Sedangkan tabung dengan jari-jari alas 15 cm dan tinggi 25 cm memiliki luas selimut tabung sebesar 1178,10 cm², luas alas tabung sebesar 706,86 cm², dan luas permukaan tabung sebesar 1884,96 cm². Dari contoh tersebut dapat dilihat bahwa semakin besar jari-jari alas tabung, semakin besar pula luas permukaan tabung.

Tinggi tabung (t)

Tinggi tabung (t) merupakan salah satu faktor yang menentukan luas permukaan tabung. Semakin tinggi tabung, semakin besar pula luas permukaan tabung. Hal ini karena tinggi tabung menentukan luas selimut tabung, yang merupakan bagian terbesar dari luas permukaan tabung.

Luas selimut tabung
Luas selimut tabung dihitung dengan rumus 2r(r+t), dimana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Semakin tinggi tabung, semakin besar pula luas selimut tabung.
Luas permukaan tabung
Luas permukaan tabung dihitung dengan rumus 2r(r+t) + 2r², dimana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Semakin tinggi tabung, semakin besar pula luas permukaan tabung.

Contohnya, sebuah tabung dengan jari-jari alas 10 cm dan tinggi 20 cm memiliki luas selimut tabung sebesar 628,32 cm² dan luas permukaan tabung sebesar 1256,64 cm². Sedangkan tabung dengan jari-jari alas 10 cm dan tinggi 25 cm memiliki luas selimut tabung sebesar 785,40 cm² dan luas permukaan tabung sebesar 1570,80 cm². Dari contoh tersebut dapat dilihat bahwa semakin tinggi tabung, semakin besar pula luas permukaan tabung.

Luas Selimut Tabung (Ls)

luas selimut tabung merupakan bagian terbesar dari luas permukaan tabung. Rumus luas selimut tabung adalah 2r(r+t), dimana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Luas selimut tabung digunakan untuk menghitung luas permukaan total tabung, yang juga meliputi luas alas dan tutup tabung.

Komponen Luas Selimut Tabung
Luas selimut tabung terdiri dari dua buah bidang lengkung yang berbentuk persegi panjang. Kedua bidang lengkung tersebut memiliki ukuran yang sama, yaitu tinggi tabung (t) dan keliling alas tabung (2r).

Contoh dalam Kehidupan Nyata
Luas selimut tabung dapat diaplikasikan dalam kehidupan nyata, seperti untuk menghitung luas permukaan kaleng minuman, pipa saluran air, dan tangki penyimpanan bahan bakar.

Implikasinya dalam Luas Permukaan Tabung
Luas selimut tabung merupakan bagian terbesar dari luas permukaan tabung. Oleh karena itu, luas selimut tabung sangat berpengaruh terhadap luas permukaan tabung secara keseluruhan.
Pengaruh Jari-jari Alas dan Tinggi Tabung
Luas selimut tabung dipengaruhi oleh jari-jari alas dan tinggi tabung. Semakin besar jari-jari alas atau tinggi tabung, semakin besar pula luas selimut tabung.

Contoh Perhitungan
Sebuah tabung dengan jari-jari alas 10 cm dan tinggi 20 cm memiliki luas selimut tabung sebesar 628,32 cm².

Implikasinya dalam Luas Permukaan Tabung
Luas selimut tabung berbanding lurus dengan jari-jari alas dan tinggi tabung. Artinya, jika jari-jari alas atau tinggi tabung diperbesar, maka luas selimut tabung juga akan membesar.
Aplikasi dalam Bidang Teknik
Luas selimut tabung banyak digunakan dalam bidang teknik, seperti untuk menghitung luas permukaan pipa, tangki, dan boiler.

Contoh Aplikasi
Seorang insinyur ingin menghitung luas permukaan pipa dengan jari-jari alas 5 cm dan tinggi 10 cm. Luas selimut tabung pipa tersebut adalah 314,16 cm².

Implikasinya dalam Luas Permukaan Tabung
Luas selimut tabung sangat penting dalam bidang teknik untuk menghitung luas permukaan benda-benda berbentuk tabung.
Hubungan dengan Luas Permukaan Tabung
Luas selimut tabung merupakan salah satu komponen dari luas permukaan tabung. Luas permukaan tabung dihitung dengan menjumlahkan luas selimut tabung dengan dua kali luas alas tabung.

Rumus Luas Permukaan Tabung
L = 2r(r+t) + 2r²

Implikasinya dalam Luas Permukaan Tabung
Luas selimut tabung sangat berpengaruh terhadap luas permukaan tabung secara keseluruhan. Semakin besar luas selimut tabung, semakin besar pula luas permukaan tabung.

Dengan memahami luas selimut tabung dan implikasinya dalam luas permukaan tabung, kita dapat menghitung luas permukaan tabung dengan lebih mudah dan akurat. Luas permukaan tabung sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran.

Luas Alas Tabung (La)

Luas alas tabung (La) merupakan salah satu komponen dari luas permukaan tabung. Luas alas tabung dihitung dengan rumus r², dimana r adalah jari-jari alas tabung. Luas alas tabung sangat penting dalam menentukan luas permukaan tabung secara keseluruhan.

Secara matematis, hubungan antara luas alas tabung dan luas permukaan tabung dapat dilihat dari rumus luas permukaan tabung, yaitu:

L = 2r(r+t) + 2r²

Dari rumus tersebut, dapat dilihat bahwa luas alas tabung (r²) merupakan salah satu suku dalam rumus luas permukaan tabung. Artinya, luas alas tabung berpengaruh terhadap luas permukaan tabung secara keseluruhan.

Dalam kehidupan nyata, luas alas tabung sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran. Misalnya, dalam teknik, luas alas tabung digunakan untuk menghitung luas permukaan pipa, tangki, dan boiler. Dalam arsitektur, luas alas tabung digunakan untuk menghitung luas permukaan kubah dan menara. Dalam kedokteran, luas alas tabung digunakan untuk menghitung luas permukaan paru-paru dan pembuluh darah.

Dengan memahami hubungan antara luas alas tabung dan luas permukaan tabung, kita dapat menghitung luas permukaan tabung dengan lebih mudah dan akurat. Luas permukaan tabung sangat penting dalam berbagai bidang, sehingga pemahaman tentang komponen-komponennya, termasuk luas alas tabung, sangat penting.

Rumus Luas Permukaan Tabung (L = 2r(r+t) + 2r)

Rumus luas permukaan tabung (L = 2r(r+t) + 2r) merupakan rumus yang sangat penting untuk menghitung luas permukaan tabung. Rumus ini terdiri dari beberapa komponen, yaitu:

r: jari-jari alas tabung
t: tinggi tabung
: konstanta matematika yang bernilai sekitar 3,14

Komponen-komponen tersebut saling berkaitan dan membentuk rumus luas permukaan tabung. Dengan menggunakan rumus ini, kita dapat menghitung luas permukaan tabung dengan mudah dan akurat.

Rumus luas permukaan tabung memiliki beberapa kegunaan dalam kehidupan nyata, di antaranya:

Menghitung luas permukaan pipa
Menghitung luas permukaan tangki
Menghitung luas permukaan boiler
Menghitung luas permukaan kubah
Menghitung luas permukaan menara

Dengan memahami rumus luas permukaan tabung dan kegunaannya, kita dapat menyelesaikan berbagai permasalahan yang berkaitan dengan luas permukaan tabung.

Aplikasi Luas Permukaan Tabung

Luas permukaan tabung memiliki berbagai aplikasi penting dalam berbagai bidang, di antaranya:

Teknik:Menghitung luas permukaan pipa, tangki, dan boiler.
Arsitektur: Menghitung luas permukaan kubah dan menara.
Kedokteran: Menghitung luas permukaan paru-paru dan pembuluh darah.

Memahami aplikasi luas permukaan tabung sangat penting karena memungkinkan kita untuk menyelesaikan berbagai permasalahan praktis. Misalnya, dalam teknik, mengetahui luas permukaan tabung sangat penting untuk merancang dan membangun struktur yang aman dan efisien. Dalam arsitektur, mengetahui luas permukaan tabung sangat penting untuk merancang dan membangun bangunan yang indah dan fungsional. Dalam kedokteran, mengetahui luas permukaan tabung sangat penting untuk mendiagnosis dan mengobati berbagai penyakit.

Sejarah Luas Permukaan Tabung

Sejarah luas permukaan tabung tidak dapat dilepaskan dari perkembangan matematika secara keseluruhan. Konsep luas permukaan tabung pertama kali ditemukan oleh matematikawan Yunani, Archimedes, pada abad ke-3 SM. Archimedes menggunakan metode penghabisan untuk menghitung luas permukaan tabung, dan menemukan rumus yang masih digunakan hingga saat ini.

Penemuan Archimedes sangat penting dalam pengembangan matematika dan fisika. Rumus luas permukaan tabung digunakan dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran. Dalam teknik, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan pipa, tangki, dan boiler. Dalam arsitektur, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan kubah dan menara. Dalam kedokteran, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan paru-paru dan pembuluh darah.

Memahami sejarah luas permukaan tabung sangat penting karena memungkinkan kita untuk menghargai perkembangan matematika dan fisika. Selain itu, memahami sejarah luas permukaan tabung juga membantu kita untuk memahami konsep luas permukaan tabung secara lebih mendalam dan menerapkannya dalam berbagai bidang praktis.

Pertanyaan Umum tentang Luas Permukaan Tabung

Berikut adalah beberapa pertanyaan umum tentang luas permukaan tabung beserta jawabannya:

Pertanyaan 1: Bagaimana cara menghitung luas permukaan tabung?

Luas permukaan tabung dihitung menggunakan rumus L = 2r(r+t) + 2r², di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung.

Pertanyaan 2: Apa saja aplikasi luas permukaan tabung dalam kehidupan nyata?

Luas permukaan tabung memiliki berbagai aplikasi dalam kehidupan nyata, seperti menghitung luas permukaan pipa, tangki, boiler, kubah, menara, paru-paru, dan pembuluh darah.

Pertanyaan 3: Siapa yang pertama kali menemukan rumus luas permukaan tabung?

Rumus luas permukaan tabung pertama kali ditemukan oleh matematikawan Yunani, Archimedes, pada abad ke-3 SM.

Pertanyaan 4: Apa pentingnya memahami luas permukaan tabung?

Memahami luas permukaan tabung sangat penting karena memungkinkan kita untuk menghitung luas permukaan berbagai objek berbentuk tabung, seperti pipa, tangki, boiler, kubah, menara, paru-paru, dan pembuluh darah.

Dengan memahami konsep dan aplikasi luas permukaan tabung, kita dapat menyelesaikan berbagai permasalahan praktis di berbagai bidang, seperti teknik, arsitektur, dan kedokteran.

Tips untuk Menghitung Luas Permukaan Tabung

Untuk menghitung luas permukaan tabung dengan akurat, ikuti tips berikut:

Pastikan Anda memiliki nilai jari-jari alas tabung (r) dan tinggi tabung (t) yang benar.
Gunakan rumus L = 2r(r+t) + 2r² dengan tepat.
Pastikan satuan yang digunakan untuk r dan t konsisten (misalnya, keduanya dalam sentimeter atau keduanya dalam meter).
Periksa kembali perhitungan Anda untuk memastikan tidak ada kesalahan.

Tips Menghitung Luas Permukaan Tabung

Berikut adalah beberapa tips penting untuk menghitung luas permukaan tabung secara akurat:

Pastikan Anda memiliki nilai jari-jari alas tabung (r) dan tinggi tabung (t) yang benar.
Nilai r dan t harus diukur dengan tepat untuk mendapatkan hasil perhitungan yang akurat. Gunakan alat ukur yang sesuai, seperti penggaris atau jangka sorong.

Gunakan rumus L = 2r(r+t) + 2r² dengan tepat.
Ikuti rumus ini dengan cermat dan pastikan setiap suku dihitung dengan benar. Perhatikan urutan operasi matematika dan gunakan tanda kurung jika diperlukan.

Pastikan satuan yang digunakan untuk r dan t konsisten.
Satuan yang digunakan untuk r dan t harus sama. Misalnya, jika r diukur dalam sentimeter, maka t juga harus diukur dalam sentimeter. Menggunakan satuan yang berbeda dapat menyebabkan kesalahan perhitungan.

Periksa kembali perhitungan Anda untuk memastikan tidak ada kesalahan.
Setelah selesai menghitung, periksa kembali setiap langkah untuk memastikan tidak ada kesalahan. Periksa kembali nilai r dan t yang Anda gunakan, serta perhitungan matematika Anda. Kesalahan kecil dapat menyebabkan hasil yang tidak akurat.

Dengan mengikuti tips ini, Anda dapat menghitung luas permukaan tabung dengan akurat dan percaya diri. Luas permukaan tabung merupakan besaran penting dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran. Memahami konsep dan metode perhitungannya sangat penting untuk menyelesaikan berbagai permasalahan praktis.

Kesimpulan

Luas permukaan tabung merupakan besaran penting yang banyak digunakan dalam berbagai bidang, seperti teknik, arsitektur, dan kedokteran. Konsep luas permukaan tabung tidak dapat dilepaskan dari perkembangan matematika dan fisika, khususnya penemuan Archimedes pada abad ke-3 SM.

Rumus luas permukaan tabung, yaitu L = 2r(r+t) + 2r², memungkinkan kita untuk menghitung luas permukaan berbagai objek berbentuk tabung dengan mudah dan akurat. Memahami konsep dan aplikasi luas permukaan tabung sangat penting untuk menyelesaikan berbagai permasalahan praktis, seperti menghitung luas permukaan pipa, tangki, boiler, kubah, menara, paru-paru, dan pembuluh darah.

Dengan terus mengeksplorasi dan mengembangkan konsep luas permukaan tabung, kita dapat terus memajukan berbagai bidang ilmu pengetahuan dan teknologi, serta memberikan kontribusi yang berarti bagi kehidupan manusia.