Intip 7 Trik Rumus Volume Kerucut yang Bikin Kamu Penasaran

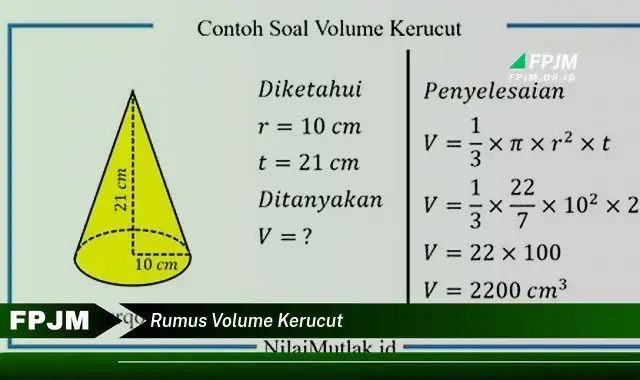
Rumus volume kerucut adalah persamaan matematika yang digunakan untuk menghitung volume bangun ruang kerucut. Rumus ini dinyatakan sebagai:

V = (1/3) r * t

di mana:

• V adalah volume kerucut dalam satuan kubik
• adalah konstanta matematika sekitar 3,14
• r adalah jari-jari alas kerucut dalam satuan panjang
• t adalah tinggi kerucut dalam satuan panjang

Rumus volume kerucut sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Rumus ini digunakan untuk menghitung volume benda-benda berbentuk kerucut, seperti corong, gelas, dan kerucut lalu lintas. Selain itu, rumus ini juga digunakan dalam kalkulus dan fisika untuk menghitung volume benda-benda yang lebih kompleks.

Dalam artikel ini, kita akan membahas secara lebih mendalam tentang rumus volume kerucut, termasuk cara penggunaannya, pentingnya, dan aplikasi-aplikasinya dalam kehidupan nyata.

rumus volume kerucut

Rumus volume kerucut merupakan persamaan matematika penting yang digunakan untuk menghitung volume bangun ruang berbentuk kerucut. Rumus ini memiliki beberapa aspek penting yang perlu dipahami, antara lain:

• Definisi: Persamaan matematika untuk menghitung volume kerucut
• Bentuk: V = (1/3) r * t
• Variabel: V (volume), (konstanta ), r (jari-jari alas), t (tinggi)
• Aplikasi: Menghitung volume benda berbentuk kerucut, seperti corong, gelas, dan kerucut lalu lintas
• Sejarah: Ditemukan oleh matematikawan Yunani kuno Archimedes
• Kalkulus: Digunakan dalam kalkulus untuk menghitung volume benda putar yang berbentuk kerucut
• Dimensi: Satuan volume (kubik) dan satuan panjang (jari-jari dan tinggi)

Semua aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang rumus volume kerucut. Sebagai contoh, definisi rumus menjelaskan tujuan dan penggunaannya, sedangkan bentuk rumus menunjukkan hubungan matematis antara volume, jari-jari, dan tinggi kerucut. Variabel dalam rumus menunjukkan besaran yang perlu diketahui untuk menghitung volume, dan aplikasi rumus menunjukkan kegunaannya dalam berbagai bidang. Sementara itu, sejarah rumus memberikan konteks tentang asal-usulnya, dan kalkulus menunjukkan hubungannya dengan konsep matematika yang lebih tinggi. Terakhir, dimensi rumus menunjukkan satuan yang digunakan untuk menyatakan volume dan besaran lainnya.

Definisi

Definisi rumus volume kerucut sebagai persamaan matematika untuk menghitung volume bangun ruang berbentuk kerucut menjadi dasar penting dalam memahami konsep dan aplikasi rumus ini. Rumus ini memiliki beberapa aspek atau komponen yang saling terkait dan membentuk pemahaman yang komprehensif tentang rumus volume kerucut.

• Komponen Rumus:

  Rumus volume kerucut terdiri dari tiga komponen utama, yaitu volume (V), konstanta , jari-jari alas (r), dan tinggi kerucut (t). Masing-masing komponen ini memiliki peran penting dalam menentukan volume kerucut.

• Relasi Matematika:

  Rumus volume kerucut menunjukkan relasi matematika antara volume kerucut dengan jari-jari alas dan tingginya. Relasi ini dinyatakan dalam bentuk persamaan V = (1/3) r * t, yang menunjukkan bahwa volume kerucut berbanding lurus dengan jari-jari alas kuadrat dan tingginya.

• Aplikasi Nyata:

  Rumus volume kerucut memiliki banyak aplikasi nyata dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Rumus ini digunakan untuk menghitung volume benda-benda berbentuk kerucut, seperti corong, gelas, dan kerucut lalu lintas.

• Konteks Sejarah:

  Rumus volume kerucut pertama kali ditemukan oleh matematikawan Yunani kuno Archimedes. Penemuan ini menjadi dasar penting dalam perkembangan matematika dan geometri.

Dengan memahami definisi dan komponen rumus volume kerucut, kita dapat memahami konsep dan aplikasi rumus ini secara lebih mendalam. Rumus ini menjadi alat penting dalam berbagai bidang untuk menghitung volume benda-benda berbentuk kerucut dengan akurat dan efisien.

Bentuk

Bentuk rumus volume kerucut, yaitu V = (1/3) r t, memiliki peranan penting dalam menentukan volume kerucut. Rumus ini merupakan persamaan matematika yang menunjukkan hubungan antara volume kerucut dengan jari-jari alas dan tingginya.

Komponen-komponen dalam rumus tersebut memiliki makna geometris yang jelas. Variabel V mewakili volume kerucut, adalah konstanta matematika sekitar 3,14, r adalah jari-jari alas kerucut, dan t adalah tinggi kerucut. Relasi matematika yang dinyatakan dalam rumus menunjukkan bahwa volume kerucut berbanding lurus dengan jari-jari alas kuadrat dan tingginya.

Sebagai contoh, jika kita memiliki sebuah kerucut dengan jari-jari alas 5 cm dan tinggi 10 cm, maka volumenya dapat dihitung menggunakan rumus V = (1/3) 5^2 * 10 = 261,80 cm. Perhitungan ini menunjukkan bahwa bentuk rumus volume kerucut memungkinkan kita untuk menentukan volume kerucut secara akurat dan efisien.

Variabel

Dalam rumus volume kerucut, terdapat beberapa variabel penting yang saling berkaitan, yaitu V (volume), (konstanta ), r (jari-jari alas), dan t (tinggi). Variabel-variabel ini merupakan komponen penyusun rumus dan memiliki peran penting dalam menentukan volume kerucut.

Variabel V mewakili volume kerucut, yang merupakan besaran yang ingin dicari. Volume kerucut dipengaruhi oleh jari-jari alas dan tingginya. Semakin besar jari-jari alas atau tinggi kerucut, maka volume kerucut akan semakin besar.

Konstanta merupakan bilangan irasional sekitar 3,14. Konstanta ini muncul dalam rumus volume kerucut karena bentuk kerucut yang menyerupai lingkaran. Jari-jari alas kerucut (r) dan tinggi kerucut (t) merupakan besaran yang harus diketahui untuk dapat menghitung volume kerucut.

Dengan memahami hubungan antara variabel-variabel dalam rumus volume kerucut, kita dapat menghitung volume kerucut dengan akurat dan efisien. Rumus ini memiliki banyak aplikasi dalam berbagai bidang, seperti teknik, arsitektur, dan desain.

Aplikasi

Rumus volume kerucut memiliki banyak aplikasi dalam kehidupan nyata. Salah satu aplikasi pentingnya adalah untuk menghitung volume benda-benda berbentuk kerucut, seperti corong, gelas, dan kerucut lalu lintas.

• Mengukur Volume Corong: Corong banyak digunakan dalam berbagai bidang, seperti laboratorium, dapur, dan industri. Dengan menggunakan rumus volume kerucut, kita dapat menentukan volume cairan atau bahan lainnya yang dapat ditampung oleh corong.
• Menghitung Kapasitas Gelas: Gelas berbentuk kerucut sering digunakan untuk menyajikan minuman. Rumus volume kerucut memungkinkan kita untuk menghitung kapasitas gelas dan menentukan jumlah minuman yang dapat ditampungnya.
• Menentukan Volume Kerucut Lalu Lintas: Kerucut lalu lintas digunakan untuk mengarahkan lalu lintas di jalan raya. Dengan menggunakan rumus volume kerucut, kita dapat menghitung volume kerucut lalu lintas dan memperkirakan jumlah bahan yang dibutuhkan untuk membuatnya.

Aplikasi-aplikasi ini menunjukkan bahwa rumus volume kerucut memiliki peran penting dalam berbagai bidang. Dengan memahami dan menerapkan rumus ini, kita dapat memecahkan masalah yang berkaitan dengan volume benda berbentuk kerucut secara akurat dan efisien.

Sejarah

Penemuan rumus volume kerucut oleh matematikawan Yunani kuno Archimedes menjadi tonggak penting dalam sejarah matematika. Archimedes menggunakan metode yang dikenal sebagai “metode penghabisan” untuk menurunkan rumus ini. Metode ini melibatkan pembagian kerucut menjadi irisan-irisan yang tak terhingga banyaknya, kemudian menghitung volume masing-masing irisan dan menjumlahkannya untuk mendapatkan volume keseluruhan kerucut.

Penemuan rumus volume kerucut memiliki implikasi yang luas dalam berbagai bidang. Rumus ini memungkinkan para ahli matematika dan ilmuwan untuk menghitung volume benda-benda berbentuk kerucut dengan akurat, yang sangat penting dalam bidang teknik, arsitektur, dan fisika. Misalnya, rumus ini digunakan untuk menghitung volume tangki berbentuk kerucut, kapasitas gelas berbentuk kerucut, dan volume benda putar yang berbentuk kerucut.

Pemahaman tentang sejarah penemuan rumus volume kerucut memberikan apresiasi terhadap kontribusi penting matematikawan kuno terhadap perkembangan ilmu pengetahuan. Selain itu, pemahaman ini juga membantu kita memahami dasar-dasar matematika dan pentingnya metode matematika dalam memecahkan masalah dunia nyata.

Kalkulus

Rumus volume kerucut memiliki hubungan yang erat dengan kalkulus, khususnya dalam konteks menghitung volume benda putar yang berbentuk kerucut. Kalkulus adalah cabang matematika yang mempelajari perubahan dan laju perubahan. Dalam konteks ini, kalkulus digunakan untuk menentukan volume benda putar yang terbentuk ketika sebuah bidang datar berbentuk segitiga siku-siku diputar mengelilingi salah satu kakinya.

Jika kita memiliki sebuah segitiga siku-siku dengan alas r dan tinggi t, dan segitiga tersebut diputar mengelilingi alasnya, maka akan terbentuk sebuah benda putar berbentuk kerucut. Volume benda putar ini dapat dihitung menggunakan rumus integral yang melibatkan rumus volume kerucut. Integral ini merepresentasikan penjumlahan volume semua irisan tipis berbentuk kerucut yang menyusun benda putar tersebut.

Perhitungan volume benda putar menggunakan kalkulus sangat penting dalam berbagai aplikasi, seperti teknik, fisika, dan desain. Misalnya, rumus ini digunakan untuk menghitung volume tangki bahan bakar roket yang berbentuk kerucut, kapasitas pipa air yang berbentuk kerucut, dan volume benda-benda aerodinamis seperti kerucut hidung pesawat terbang.

Dengan memahami hubungan antara kalkulus dan rumus volume kerucut, kita dapat memecahkan masalah yang lebih kompleks yang melibatkan volume benda putar. Kalkulus memberikan alat yang ampuh untuk menghitung volume benda-benda yang bentuknya tidak beraturan atau tidak dapat dihitung secara langsung menggunakan rumus geometri dasar.

Dimensi

Dimensi dari rumus volume kerucut memainkan peran penting dalam menentukan dan menginterpretasikan hasilnya. Rumus ini melibatkan besaran volume, jari-jari alas, dan tinggi kerucut, yang masing-masing memiliki satuan yang berbeda.

• Satuan Volume:
  Volume kerucut dinyatakan dalam satuan kubik, seperti sentimeter kubik (cm), meter kubik (m), atau liter (L). Satuan ini menunjukkan kapasitas atau ruang yang ditempati oleh kerucut.
• Satuan Panjang:
  Jari-jari alas dan tinggi kerucut dinyatakan dalam satuan panjang, seperti sentimeter (cm), meter (m), atau kaki (ft). Satuan ini menunjukkan ukuran atau dimensi linier dari kerucut.

Hubungan antara satuan volume dan satuan panjang dalam rumus volume kerucut sangat penting untuk dipahami. Rumus tersebut menunjukkan bahwa volume kerucut berbanding lurus dengan jari-jari alas kuadrat dan tingginya. Oleh karena itu, perubahan satuan panjang akan mempengaruhi nilai volume kerucut.

Memahami dimensi dari rumus volume kerucut sangat penting untuk memastikan akurasi dan konsistensi dalam perhitungan volume kerucut. Selain itu, pemahaman ini juga membantu dalam mengonversi antara satuan volume yang berbeda, seperti mengubah liter menjadi sentimeter kubik atau meter kubik.

Pertanyaan Umum Tentang Rumus Volume Kerucut

Berikut adalah beberapa pertanyaan umum dan jawabannya mengenai rumus volume kerucut:

Pertanyaan 1: Bagaimana cara menggunakan rumus volume kerucut?

Untuk menggunakan rumus volume kerucut, Anda perlu mengetahui tiga besaran berikut: jari-jari alas kerucut, tinggi kerucut, dan konstanta . Rumus volume kerucut adalah V = (1/3) r * t, di mana V adalah volume kerucut, adalah konstanta sekitar 3,14, r adalah jari-jari alas kerucut, dan t adalah tinggi kerucut.

Pertanyaan 2: Mengapa konstanta digunakan dalam rumus volume kerucut?

Konstanta digunakan dalam rumus volume kerucut karena bentuk kerucut menyerupai lingkaran. Lingkaran memiliki sifat matematis tertentu, termasuk keliling dan luas, yang melibatkan konstanta .

Pertanyaan 3: Apa saja aplikasi dari rumus volume kerucut?

Rumus volume kerucut memiliki banyak aplikasi dalam berbagai bidang, antara lain teknik, arsitektur, dan desain. Rumus ini digunakan untuk menghitung volume benda-benda berbentuk kerucut, seperti corong, gelas, dan kerucut lalu lintas.

Pertanyaan 4: Bagaimana rumus volume kerucut terkait dengan kalkulus?

Rumus volume kerucut terkait dengan kalkulus dalam konteks menghitung volume benda putar yang berbentuk kerucut. Kalkulus digunakan untuk menentukan volume benda putar yang terbentuk ketika sebuah bidang datar berbentuk segitiga siku-siku diputar mengelilingi salah satu kakinya.

Dengan memahami pertanyaan umum ini dan jawabannya, Anda dapat memperoleh pemahaman yang lebih baik tentang rumus volume kerucut dan penggunaannya dalam berbagai aplikasi.

Selain itu, tips berikut dapat membantu Anda dalam memahami dan menerapkan rumus volume kerucut secara efektif:

Tips Menggunakan Rumus Volume Kerucut

Tips Menggunakan Rumus Volume Kerucut

Berikut adalah beberapa tips yang dapat membantu Anda dalam memahami dan menerapkan rumus volume kerucut secara efektif:

Tip 1: Pahami Konsep Kerucut
Sebelum menggunakan rumus volume kerucut, pastikan Anda memahami konsep kerucut sebagai bangun ruang yang berbentuk seperti corong. Kerucut memiliki alas berbentuk lingkaran dan satu titik puncak yang disebut titik puncak kerucut.

Tip 2: Identifikasi Besaran yang Diketahui dan Tidak Diketahui
Rumus volume kerucut membutuhkan tiga besaran, yaitu jari-jari alas, tinggi kerucut, dan volume kerucut. Identifikasi besaran yang diketahui dan tidak diketahui sebelum menggunakan rumus.

Tip 3: Gunakan Satuan yang Konsisten
Pastikan Anda menggunakan satuan yang konsisten untuk jari-jari alas dan tinggi kerucut. Umumnya, satuan sentimeter atau meter digunakan. Jika satuan berbeda, konversikan terlebih dahulu ke satuan yang sama.

Tip 4: Periksa Kembali Hasil Perhitungan
Setelah menghitung volume kerucut, periksa kembali hasil perhitungan Anda untuk memastikan kebenarannya. Anda dapat melakukan pengecekan dengan membandingkan hasil Anda dengan contoh soal atau menggunakan kalkulator online.

Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman dan keterampilan Anda dalam menggunakan rumus volume kerucut untuk menyelesaikan masalah yang berkaitan dengan bangun ruang kerucut.

Setelah memahami tips ini, Anda dapat melanjutkan ke bagian selanjutnya untuk mempelajari lebih lanjut tentang aplikasi rumus volume kerucut dalam berbagai bidang.

Kesimpulan

Rumus volume kerucut merupakan rumus matematika penting yang digunakan untuk menghitung volume bangun ruang berbentuk kerucut. Rumus ini memiliki peran penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Dengan memahami konsep, aplikasi, dan penggunaan rumus volume kerucut, kita dapat memecahkan masalah yang berkaitan dengan volume benda berbentuk kerucut secara akurat dan efisien.

Selain itu, rumus volume kerucut memiliki hubungan erat dengan kalkulus dalam konteks menghitung volume benda putar yang berbentuk kerucut. Pemahaman tentang hubungan ini memungkinkan kita untuk menyelesaikan masalah yang lebih kompleks yang melibatkan volume benda-benda yang bentuknya tidak beraturan. Dengan terus mengeksplorasi dan mengaplikasikan rumus volume kerucut, kita dapat memperoleh pemahaman yang lebih mendalam tentang konsep matematika dan penerapannya dalam kehidupan nyata.