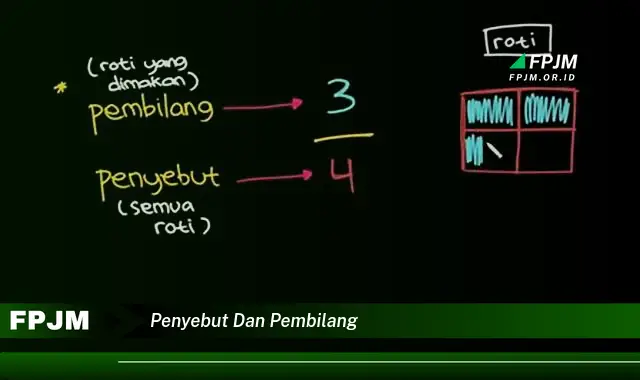
Dalam matematika, penyebut dan pembilang adalah dua bagian dari pecahan. Penyebut adalah angka di bagian bawah pecahan, dan pembilang adalah angka di bagian atas pecahan. Misalnya, dalam pecahan 1/2, 2 adalah penyebut dan 1 adalah pembilang.
Penyebut dan pembilang sangat penting dalam matematika. Penyebut menunjukkan berapa banyak bagian yang sama menjadi keseluruhan, dan pembilang menunjukkan berapa banyak bagian yang diambil. Misalnya, pecahan 1/2 menunjukkan bahwa keseluruhan dibagi menjadi 2 bagian yang sama, dan 1 bagian diambil. Penyebut dan pembilang juga digunakan untuk melakukan operasi matematika, seperti penjumlahan, pengurangan, perkalian, dan pembagian pecahan.
Konsep penyebut dan pembilang telah digunakan selama berabad-abad. Pecahan pertama kali ditemukan di Mesir Kuno sekitar 3000 SM. Sejak saat itu, pecahan telah digunakan dalam berbagai bidang, termasuk perdagangan, pertanian, dan teknik.
Penyebut dan Pembilang
Penyebut dan pembilang adalah dua bagian penting dari pecahan. Penyebut menunjukkan banyaknya bagian yang sama menjadi keseluruhan, dan pembilang menunjukkan banyaknya bagian yang diambil. Berikut adalah 7 aspek penting terkait penyebut dan pembilang:
- Bagian pecahan
- Menunjukkan nilai
- Operasi matematika
- Penyederhanaan
- Bilangan bulat
- Pecahan campuran
- Persamaan
Ketujuh aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang penyebut dan pembilang. Misalnya, kita dapat menggunakan penyebut dan pembilang untuk melakukan operasi matematika seperti penjumlahan dan pengurangan pecahan. Kita juga dapat menyederhanakan pecahan dengan mencari faktor persekutuan terbesar dari penyebut dan pembilang. Selain itu, penyebut dan pembilang juga dapat digunakan untuk mengubah pecahan menjadi bilangan bulat atau pecahan campuran. Pemahaman yang baik tentang aspek-aspek ini sangat penting untuk menguasai konsep pecahan.
Bagian Pecahan
Dalam matematika, pecahan adalah bilangan yang menyatakan bagian dari keseluruhan. Pecahan terdiri dari dua bagian utama, yaitu penyebut dan pembilang.
-
Penyebut
Penyebut terletak di bagian bawah pecahan dan menunjukkan banyaknya bagian yang sama menjadi keseluruhan. Misalnya, dalam pecahan 1/2, penyebutnya adalah 2, yang berarti keseluruhan dibagi menjadi 2 bagian yang sama. -
Pembilang
Pembilang terletak di bagian atas pecahan dan menunjukkan banyaknya bagian yang diambil dari keseluruhan. Misalnya, dalam pecahan 1/2, pembilangnya adalah 1, yang berarti 1 bagian dari 2 bagian yang sama diambil.
Penyebut dan pembilang sangat penting karena menentukan nilai pecahan. Semakin besar penyebutnya, semakin kecil nilai pecahannya. Sebaliknya, semakin besar pembilangnya, semakin besar nilai pecahannya.
Menunjukkan Nilai
Penyebut dan pembilang memainkan peran penting dalam menunjukkan nilai pecahan. Penyebut menunjukkan banyaknya bagian yang sama menjadi keseluruhan, sedangkan pembilang menunjukkan banyaknya bagian yang diambil dari keseluruhan. Dari informasi ini, kita dapat menentukan nilai pecahan.
Sebagai contoh, perhatikan pecahan 3/4. Penyebut 4 menunjukkan bahwa keseluruhan dibagi menjadi 4 bagian yang sama. Pembilang 3 menunjukkan bahwa 3 bagian dari 4 bagian yang sama diambil. Dari informasi ini, kita dapat menentukan bahwa nilai pecahan 3/4 adalah 3/4 atau 0,75.
Memahami bagaimana penyebut dan pembilang menunjukkan nilai pecahan sangat penting untuk melakukan operasi matematika yang melibatkan pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Dengan memahami konsep ini, kita dapat menyelesaikan masalah matematika yang melibatkan pecahan secara akurat dan efisien.
Operasi Matematika
Dalam matematika, operasi matematika merupakan tindakan yang dilakukan terhadap bilangan atau variabel untuk menghasilkan nilai baru. Dalam konteks penyebut dan pembilang, operasi matematika memegang peranan penting dalam memanipulasi dan menyelesaikan pecahan.
-
Penjumlahan dan Pengurangan
Penjumlahan dan pengurangan pecahan melibatkan operasi pada penyebut dan pembilang. Untuk menjumlahkan atau mengurangkan pecahan dengan penyebut berbeda, penyebut harus disamakan terlebih dahulu. -
Perkalian
Ketika mengalikan pecahan, penyebut dikalikan dengan penyebut dan pembilang dikalikan dengan pembilang. Hasil perkalian dua pecahan adalah pecahan baru dengan penyebut hasil kali penyebut kedua pecahan dan pembilang hasil kali pembilang kedua pecahan. -
Pembagian
Pembagian pecahan melibatkan pembalikan pecahan kedua (penyebut dan pembilang ditukar) dan kemudian mengalikannya dengan pecahan pertama. Hasil bagi dua pecahan adalah pecahan baru dengan penyebut hasil kali penyebut kedua pecahan dan pembilang hasil kali pembilang kedua pecahan. -
Penyederhanaan
Penyederhanaan pecahan bertujuan untuk memperoleh pecahan yang setara dengan nilai yang lebih sederhana. Penyebut dan pembilang dibagi dengan faktor persekutuan terbesar (FPB) untuk memperoleh pecahan yang lebih sederhana.
Operasi matematika pada penyebut dan pembilang sangat penting untuk menyelesaikan berbagai permasalahan matematika yang melibatkan pecahan. Dengan memahami operasi-operasi ini, kita dapat memanipulasi pecahan untuk memperoleh hasil yang diinginkan.
Penyederhanaan
Penyederhanaan pecahan merupakan proses memperoleh pecahan yang setara dengan nilai yang lebih sederhana. Dalam konteks penyebut dan pembilang, penyederhanaan berperan penting untuk memperoleh pecahan yang lebih mudah dipahami dan digunakan dalam operasi matematika.
Untuk menyederhanakan pecahan, kita perlu mencari faktor persekutuan terbesar (FPB) dari penyebut dan pembilang. FPB merupakan faktor terbesar yang membagi habis baik penyebut maupun pembilang. Setelah menemukan FPB, kita bagi penyebut dan pembilang dengan FPB tersebut. Hasilnya adalah pecahan yang lebih sederhana.
Penyederhanaan pecahan sangat penting karena memiliki beberapa manfaat praktis. Pertama, penyederhanaan memudahkan kita untuk membandingkan pecahan. Pecahan yang lebih sederhana akan lebih mudah dibandingkan dengan pecahan yang lebih kompleks. Kedua, penyederhanaan memudahkan kita untuk melakukan operasi matematika pada pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
Sebagai contoh, mari kita sederhanakan pecahan 12/18. FPB dari 12 dan 18 adalah 6. Kita bagi penyebut dan pembilang dengan 6, sehingga diperoleh pecahan 2/3. Pecahan 2/3 adalah pecahan yang lebih sederhana dan lebih mudah digunakan dalam operasi matematika.
Bilangan Bulat
Bilangan bulat memiliki keterkaitan erat dengan penyebut dan pembilang dalam matematika. Bilangan bulat adalah bilangan yang tidak memiliki bagian pecahan, seperti -3, 0, dan 7. Sedangkan penyebut dan pembilang digunakan untuk menyatakan pecahan, yang merupakan bagian dari keseluruhan.
-
Representasi Pecahan
Bilangan bulat dapat digunakan untuk merepresentasikan pecahan dengan penyebut 1. Misalnya, bilangan bulat 3 dapat ditulis sebagai pecahan 3/1, yang menunjukkan 3 bagian dari keseluruhan.
-
Penyebut Bersama
Ketika menjumlahkan atau mengurangkan pecahan dengan penyebut berbeda, bilangan bulat dapat digunakan sebagai penyebut bersama. Penyebut bersama adalah kelipatan dari kedua penyebut asli, yang memungkinkan penjumlahan atau pengurangan pecahan dengan mudah.
-
Pembagian Pecahan
Dalam pembagian pecahan, bilangan bulat dapat digunakan untuk menyederhanakan proses. Jika pembilang atau penyebut salah satu pecahan adalah bilangan bulat, pembagian dapat dilakukan dengan cara mengalikan pecahan dengan kebalikan dari bilangan bulat tersebut.
-
Konversi Pecahan ke Bilangan Campuran
Bilangan bulat juga digunakan dalam konversi pecahan ke bilangan campuran. Bilangan campuran adalah kombinasi bilangan bulat dan pecahan. Untuk mengonversi pecahan ke bilangan campuran, kita membagi pembilang dengan penyebut dan menuliskan hasil bagi sebagai bilangan bulat, sedangkan sisanya menjadi pembilang pecahan.
Dengan memahami keterkaitan antara bilangan bulat, penyebut, dan pembilang, kita dapat memanipulasi dan menyelesaikan pecahan dengan lebih mudah. Konsep-konsep ini sangat penting dalam berbagai aspek matematika, termasuk aljabar dan kalkulus.
Pecahan Campuran
Dalam matematika, pecahan campuran merupakan kombinasi bilangan bulat dan pecahan biasa. Pecahan campuran digunakan untuk menyatakan bilangan yang lebih besar dari 1 atau bilangan yang tidak dapat dinyatakan sebagai bilangan bulat.
-
Komponen Pecahan Campuran
Pecahan campuran terdiri dari dua komponen utama, yaitu bilangan bulat dan pecahan biasa. Bilangan bulat menyatakan bagian utuh, sedangkan pecahan biasa menyatakan bagian pecahan.
-
Konversi Pecahan Biasa ke Pecahan Campuran
Untuk mengonversi pecahan biasa ke pecahan campuran, kita perlu membagi pembilang dengan penyebut. Hasil bagi merupakan bilangan bulat, sedangkan sisa menjadi pembilang pecahan pada pecahan campuran.
-
Operasi Matematika pada Pecahan Campuran
Operasi matematika pada pecahan campuran dilakukan dengan terlebih dahulu mengonversi pecahan campuran ke pecahan biasa. Setelah itu, operasi matematika dapat dilakukan seperti biasa.
-
Aplikasi Pecahan Campuran
Pecahan campuran memiliki banyak aplikasi dalam kehidupan nyata, seperti dalam pengukuran, pembagian, dan perhitungan persentase. Misalnya, dalam resep memasak, pecahan campuran digunakan untuk menyatakan jumlah bahan yang dibutuhkan.
Memahami konsep pecahan campuran sangat penting karena merupakan dasar untuk memahami operasi matematika yang lebih kompleks, seperti aljabar dan kalkulus. Selain itu, pecahan campuran juga banyak digunakan dalam berbagai bidang, seperti sains, teknik, dan ekonomi.
Persamaan
Dalam matematika, persamaan merupakan suatu pernyataan yang menyatakan bahwa dua ekspresi memiliki nilai yang sama. Penyebut dan pembilang memainkan peran penting dalam menyelesaikan persamaan yang melibatkan pecahan.
Penyebut dan pembilang digunakan untuk menyamakan penyebut pecahan di kedua sisi persamaan. Dengan menyamakan penyebut, kita dapat melakukan operasi matematika pada pecahan dengan lebih mudah, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Tanpa menyamakan penyebut, operasi matematika pada pecahan akan menjadi lebih kompleks dan sulit.
Sebagai contoh, perhatikan persamaan berikut:
$$\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$$Untuk menyelesaikan persamaan ini, kita perlu menyamakan penyebut pada kedua sisi persamaan. Penyebut terkecil yang sama dari 2 dan 3 adalah 6. Kita kalikan pembilang dan penyebut pecahan pertama dengan 3, dan pecahan kedua dengan 2:$$\frac{1}{2} \times \frac{3}{3} + \frac{1}{3} \times \frac{2}{2} = \frac{5}{6}$$$$\frac{3}{6} + \frac{2}{6} = \frac{5}{6}$$Setelah penyebut disamakan, kita dapat menjumlahkan pembilang pada kedua sisi persamaan dan memperoleh jawabannya:$$\frac{3}{6} + \frac{2}{6} = \frac{5}{6}$$$$\frac{5}{6} = \frac{5}{6}$$Dari contoh tersebut, kita dapat melihat bahwa penyebut dan pembilang sangat penting dalam menyelesaikan persamaan yang melibatkan pecahan. Dengan memahami konsep penyebut dan pembilang, kita dapat menyelesaikan persamaan tersebut dengan lebih mudah dan efisien.
Pertanyaan Umum tentang Penyebut dan Pembilang
Bagian ini menyajikan beberapa pertanyaan umum dan jawabannya terkait penyebut dan pembilang dalam matematika.
Pertanyaan 1: Apa yang dimaksud dengan penyebut dan pembilang?
Penyebut adalah bilangan di bagian bawah pecahan yang menunjukkan banyaknya bagian yang sama menjadi keseluruhan. Pembilang adalah bilangan di bagian atas pecahan yang menunjukkan banyaknya bagian yang diambil dari keseluruhan.
Pertanyaan 2: Bagaimana cara menyederhanakan pecahan?
Untuk menyederhanakan pecahan, carilah faktor persekutuan terbesar (FPB) dari penyebut dan pembilang. Kemudian, bagi penyebut dan pembilang dengan FPB tersebut.
Pertanyaan 3: Bagaimana cara menjumlahkan atau mengurangkan pecahan dengan penyebut berbeda?
Untuk menjumlahkan atau mengurangkan pecahan dengan penyebut berbeda, samakan penyebutnya terlebih dahulu. Caranya dengan mencari kelipatan persekutuan terkecil (KPK) dari penyebut-penyebut tersebut.
Pertanyaan 4: Apa saja aplikasi penyebut dan pembilang dalam kehidupan nyata?
Penyebut dan pembilang banyak digunakan dalam kehidupan nyata, seperti dalam pengukuran, pembagian, dan perhitungan persentase. Misalnya, dalam resep memasak, penyebut dan pembilang digunakan untuk menyatakan jumlah bahan yang dibutuhkan.
Kesimpulan:
Memahami konsep penyebut dan pembilang sangat penting dalam matematika. Konsep-konsep ini menjadi dasar untuk operasi matematika yang lebih kompleks dan memiliki banyak aplikasi dalam kehidupan nyata.
Lanjut ke Tips Artikel:
Untuk memperdalam pemahaman Anda tentang penyebut dan pembilang, silakan lanjutkan ke bagian tips artikel.
Tips Memahami Penyebut dan Pembilang
Untuk memperdalam pemahaman Anda tentang penyebut dan pembilang, berikut beberapa tips yang dapat membantu:
Tip 1: Visualisasikan pecahan menggunakan gambar atau diagram
Merepresentasikan pecahan secara visual dapat membantu Anda memahami konsep penyebut dan pembilang dengan lebih baik. Misalnya, Anda dapat menggunakan lingkaran yang dibagi menjadi bagian-bagian yang sama untuk menunjukkan penyebut dan mewarnai beberapa bagian untuk menunjukkan pembilang.
Tip 2: Latih operasi matematika yang melibatkan pecahan secara teratur
Melakukan operasi matematika pada pecahan secara rutin akan meningkatkan keterampilan Anda dalam memanipulasi penyebut dan pembilang. Berlatihlah menjumlahkan, mengurangkan, mengalikan, dan membagi pecahan dengan berbagai penyebut.
Tip 3: Pahami konsep faktor persekutuan terbesar (FPB) dan kelipatan persekutuan terkecil (KPK)
Konsep FPB dan KPK sangat penting untuk menyederhanakan pecahan dan menjumlahkan atau mengurangkan pecahan dengan penyebut berbeda. Pelajari cara mencari FPB dan KPK dari dua bilangan atau lebih.
Tip 4: Terapkan konsep penyebut dan pembilang dalam konteks kehidupan nyata
Menghubungkan konsep penyebut dan pembilang dengan situasi kehidupan nyata dapat membantu Anda memahami relevansinya. Misalnya, Anda dapat menggunakan pecahan untuk membagi pizza atau menghitung persentase diskon.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang penyebut dan pembilang serta menggunakannya dengan percaya diri dalam berbagai konteks.
Kesimpulan:
Memahami konsep penyebut dan pembilang sangat penting untuk menguasai matematika. Dengan memahami konsep ini, Anda akan lebih siap untuk memecahkan masalah matematika yang kompleks dan menerapkan matematika dalam situasi kehidupan nyata.
Kesimpulan
Dalam matematika, penyebut dan pembilang merupakan komponen penting dari pecahan yang menunjukkan bagian dari keseluruhan. Memahami konsep penyebut dan pembilang sangat penting untuk melakukan operasi matematika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian pecahan.
Selain itu, penyebut dan pembilang juga berperan penting dalam menyederhanakan pecahan, membandingkan pecahan, dan mengonversi pecahan ke bentuk desimal atau persen. Konsep ini banyak digunakan dalam berbagai bidang, seperti sains, teknik, dan ekonomi.
Dengan memahami penyebut dan pembilang secara mendalam, kita dapat menyelesaikan masalah matematika dengan lebih mudah dan percaya diri, serta menerapkan konsep matematika dalam berbagai konteks kehidupan nyata.




