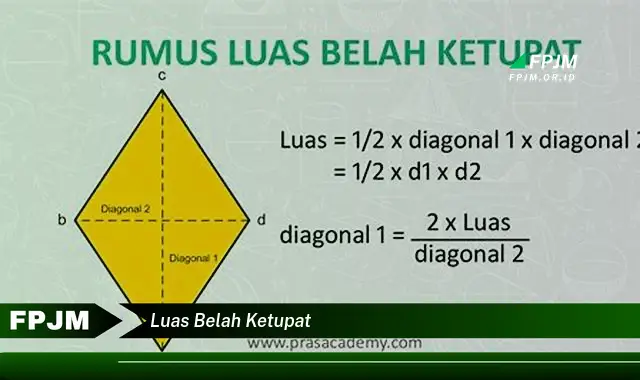
Luas belah ketupat adalah besaran yang menyatakan ukuran daerah yang ditempati oleh suatu belah ketupat. Untuk menghitung luas belah ketupat, kita dapat menggunakan rumus:
L = x d1 x d2
Dimana:
- L adalah luas belah ketupat
- d1 adalah diagonal pertama belah ketupat
- d2 adalah diagonal kedua belah ketupat
Luas belah ketupat memiliki peran penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dengan mengetahui luas suatu belah ketupat, kita dapat menentukan ukuran bahan yang dibutuhkan, menghitung biaya konstruksi, dan merencanakan tata letak ruang.
Konsep luas belah ketupat telah dikenal sejak zaman dahulu. Matematikawan Yunani, Euclid, sekitar tahun 300 SM, telah menggunakan konsep ini dalam karyanya, “The Elements”.
Pada artikel ini, kita akan membahas lebih dalam tentang luas belah ketupat, termasuk rumus untuk menghitungnya, sifat-sifatnya, dan penerapannya dalam berbagai bidang.
Luas Belah Ketupat
Luas belah ketupat merupakan besaran yang menyatakan ukuran daerah yang ditempati oleh suatu belah ketupat. Berikut adalah 7 aspek penting terkait luas belah ketupat:
- Rumus: L = x d1 x d2
- Diagonal: Diperlukan dua diagonal untuk menghitung luas.
- Satuan: Luas dinyatakan dalam satuan luas, seperti meter persegi (m).
- Sifat: Luas belah ketupat tidak berubah jika belah ketupat diputar atau dibalik.
- Aplikasi: Berguna dalam arsitektur, teknik, dan desain.
- Sejarah: Konsep luas belah ketupat telah dikenal sejak zaman Euclid.
- Contoh: Belah ketupat dengan diagonal 5 cm dan 8 cm memiliki luas 20 cm.
Ketujuh aspek ini saling terkait dan memberikan pemahaman yang komprehensif tentang luas belah ketupat. Rumus yang jelas memungkinkan kita menghitung luas dengan mudah, sementara sifat-sifatnya memberi kita wawasan tentang perilaku luas belah ketupat di bawah transformasi tertentu. Aplikasi luas belah ketupat dalam berbagai bidang menunjukkan relevansinya dalam kehidupan nyata, dan sejarahnya memberi kita apresiasi terhadap perkembangan konsep matematis ini. Dengan memahami aspek-aspek ini, kita dapat lebih menghargai pentingnya luas belah ketupat dalam matematika dan penerapannya yang luas.
Rumus
Rumus ini merupakan dasar untuk menghitung luas belah ketupat. Dengan mengetahui panjang kedua diagonalnya, kita dapat dengan mudah menentukan luasnya menggunakan rumus ini. Dalam konteks luas belah ketupat, rumus ini sangat penting karena memberikan metode yang jelas dan akurat untuk mengukur daerah yang ditempati oleh suatu belah ketupat.
- Menghitung Luas: Rumus ini memungkinkan kita menghitung luas belah ketupat dengan cepat dan efisien, yang penting dalam berbagai aplikasi praktis, seperti desain arsitektur dan perencanaan teknik.
- Diagonal Berpengaruh: Rumus ini menunjukkan bahwa luas belah ketupat bergantung pada panjang kedua diagonalnya. Ini menyoroti pentingnya diagonal dalam menentukan ukuran daerah suatu belah ketupat.
- Generalisasi: Rumus ini berlaku untuk semua belah ketupat, terlepas dari ukuran atau orientasinya. Ini menunjukkan sifat umum dari rumus dan relevansinya dalam berbagai konteks.
- Aplikasi Praktis: Rumus ini banyak digunakan dalam aplikasi praktis, seperti menghitung luas tanah, merencanakan tata letak ruangan, dan menentukan kebutuhan bahan untuk konstruksi. Ini menggarisbawahi nilai praktis dari rumus dalam kehidupan nyata.
Kesimpulannya, rumus L = x d1 x d2 sangat penting dalam konteks luas belah ketupat. Ini memberikan metode yang jelas untuk menghitung luas, menunjukkan ketergantungan pada diagonal, berlaku secara umum untuk semua belah ketupat, dan memiliki berbagai aplikasi praktis. Dengan memahami rumus ini, kita dapat lebih menghargai peran penting luas belah ketupat dalam berbagai bidang.
Diagonal
Dalam konteks luas belah ketupat, diagonal memainkan peran penting karena digunakan untuk menentukan luas tersebut. Berikut adalah beberapa detail konten yang menghubungkan diagonal dengan luas belah ketupat:
- Penentu Luas: Diagonal sangat penting dalam menentukan luas belah ketupat. Tanpa mengetahui panjang kedua diagonal, kita tidak dapat menghitung luasnya secara akurat.
- Sifat Diagonal: Sifat-sifat diagonal, seperti saling tegak lurus, digunakan dalam rumus luas belah ketupat. Ini menunjukkan keterkaitan yang mendasar antara diagonal dan luas.
- Pengukuran Praktis: Dalam aplikasi praktis, mengukur diagonal seringkali lebih mudah daripada mengukur sisi belah ketupat. Hal ini membuat penggunaan diagonal dalam menghitung luas menjadi metode yang lebih efisien.
- Generalisasi: Rumus luas belah ketupat yang menggunakan diagonal berlaku untuk semua belah ketupat, terlepas dari ukuran atau bentuknya. Ini menyoroti peran umum diagonal dalam mengukur luas belah ketupat.
Dengan memahami hubungan antara diagonal dan luas belah ketupat, kita dapat lebih menghargai pentingnya diagonal dalam menentukan luas suatu belah ketupat. Diagonal tidak hanya berfungsi sebagai alat ukur, tetapi juga mencerminkan sifat-sifat geometris dasar belah ketupat. Hal ini menyoroti saling ketergantungan antara konsep-konsep ini dan memberikan wawasan yang mendalam tentang luas belah ketupat.
Satuan
Dalam konteks luas belah ketupat, satuan sangat penting karena memungkinkan kita mengukur dan membandingkan luas belah ketupat yang berbeda. Penggunaan satuan yang konsisten memastikan komunikasi yang jelas dan pemahaman yang akurat tentang ukuran daerah suatu belah ketupat.
Satuan luas, seperti meter persegi (m), memberikan referensi standar untuk mengukur luas belah ketupat. Dengan menggunakan satuan ini, kita dapat membandingkan luas belah ketupat dengan bentuk geometris lainnya dan menentukan ukuran relatifnya. Misalnya, kita dapat mengatakan bahwa belah ketupat dengan luas 10 m lebih besar dari belah ketupat dengan luas 5 m.
Pemahaman tentang satuan luas sangat penting dalam berbagai aplikasi praktis. Dalam arsitektur, satuan luas digunakan untuk menentukan ukuran ruangan, merencanakan tata letak bangunan, dan menghitung kebutuhan bahan. Dalam teknik, satuan luas digunakan untuk menghitung luas permukaan benda, seperti pelat logam atau dinding penahan. Dalam desain lanskap, satuan luas digunakan untuk mengukur luas taman, merencanakan penanaman, dan menentukan kebutuhan irigasi.
Dengan memahami hubungan antara luas belah ketupat dan satuan luas, kita dapat lebih menghargai pentingnya satuan dalam mengukur dan membandingkan luas. Satuan luas memberikan dasar untuk komunikasi yang jelas, perbandingan yang akurat, dan aplikasi praktis yang luas.
Sifat
Sifat ini sangat penting dalam konteks luas belah ketupat karena menunjukkan bahwa luas belah ketupat tidak bergantung pada orientasinya. Berikut adalah beberapa detail konten yang menghubungkan sifat ini dengan luas belah ketupat:
- Invariansi Luas: Sifat ini menunjukkan bahwa luas belah ketupat tetap sama, tidak peduli bagaimana belah ketupat diputar atau dibalik. Ini menyoroti sifat intrinsik luas belah ketupat, yang tidak dipengaruhi oleh transformasi eksternal.
- Aplikasi Praktis: Dalam aplikasi praktis, sifat ini sangat berguna ketika kita perlu mengukur atau membandingkan luas belah ketupat dalam orientasi yang berbeda. Kita dapat yakin bahwa luasnya akan tetap sama, sehingga memudahkan untuk melakukan perhitungan dan perbandingan.
- Konsistensi Geometris: Sifat ini konsisten dengan sifat geometris belah ketupat. Belah ketupat adalah bentuk simetris dengan empat sisi yang sama panjang, dan sifat ini mencerminkan simetri dan keteraturan bentuknya.
Dengan memahami hubungan antara sifat ini dan luas belah ketupat, kita dapat lebih menghargai pentingnya sifat ini dalam menentukan dan memahami luas belah ketupat. Sifat ini memberikan dasar untuk pengukuran yang konsisten, memudahkan aplikasi praktis, dan mencerminkan sifat geometris belah ketupat.
Aplikasi
Luas belah ketupat memiliki peran penting dalam berbagai bidang praktis, khususnya dalam arsitektur, teknik, dan desain. Berikut adalah beberapa detail konten yang menghubungkan aplikasi ini dengan luas belah ketupat:
- Arsitektur: Dalam arsitektur, luas belah ketupat digunakan untuk menentukan ukuran ruangan, merencanakan tata letak bangunan, dan menghitung kebutuhan bahan. Misalnya, arsitek menggunakan rumus luas belah ketupat untuk menentukan luas lantai, luas dinding, dan luas atap suatu bangunan.
- Teknik: Dalam teknik, luas belah ketupat digunakan untuk menghitung luas permukaan benda, seperti pelat logam atau dinding penahan. Misalnya, insinyur menggunakan rumus luas belah ketupat untuk menentukan luas permukaan pelat logam yang digunakan dalam konstruksi jembatan atau luas permukaan dinding penahan yang digunakan untuk menahan tanah.
- Desain: Dalam desain, luas belah ketupat digunakan untuk menentukan ukuran objek dekoratif, seperti ubin atau pola lantai. Misalnya, desainer menggunakan rumus luas belah ketupat untuk menentukan luas ubin yang dibutuhkan untuk menutupi lantai atau luas pola lantai yang akan dibuat.
Dengan memahami hubungan antara aplikasi ini dan luas belah ketupat, kita dapat lebih menghargai pentingnya luas belah ketupat dalam berbagai bidang praktis. Luas belah ketupat memberikan dasar untuk pengukuran yang akurat, perencanaan yang efisien, dan desain yang efektif.
Sejarah
Sejarah konsep luas belah ketupat tidak terlepas dari peran penting Euclid, seorang matematikawan Yunani yang hidup pada sekitar tahun 300 SM. Dalam karyanya yang terkenal, “The Elements”, Euclid menguraikan konsep luas belah ketupat sebagai bagian dari sistem geometri yang komprehensif.
- Landasan Geometri: Konsep luas belah ketupat yang dikemukakan Euclid menjadi landasan bagi perkembangan geometri selanjutnya. Rumus yang dia berikan untuk menghitung luas belah ketupat, yaitu L = x d1 x d2, telah digunakan selama berabad-abad dan masih menjadi dasar perhitungan luas belah ketupat hingga saat ini.
- Aplikasi Praktis: Sejak zaman dahulu, konsep luas belah ketupat telah diterapkan dalam berbagai bidang praktis. Arsitek menggunakannya untuk menghitung luas bangunan dan merencanakan tata letak ruang. Insinyur menggunakannya untuk menghitung luas permukaan struktur dan menentukan kebutuhan material.
- Pengaruh pada Seni: Konsep luas belah ketupat juga memengaruhi perkembangan seni dan desain. Seniman menggunakannya untuk membuat pola dekoratif dan ubin dengan bentuk belah ketupat. Desainer menggunakannya untuk menciptakan karya seni yang harmonis dan seimbang.
Pengakuan Euclid terhadap konsep luas belah ketupat telah memberikan kontribusi yang signifikan terhadap pengembangan matematika dan berbagai bidang lainnya. Konsep ini telah menjadi dasar bagi pemahaman kita tentang bentuk geometris, pengukuran luas, dan aplikasi praktis dalam berbagai aspek kehidupan.
Contoh
Contoh ini menunjukkan bagaimana konsep luas belah ketupat diterapkan dalam situasi nyata. Dengan mengetahui panjang diagonal belah ketupat, kita dapat menghitung luasnya menggunakan rumus L = x d1 x d2. Dalam contoh ini, diagonal memiliki panjang 5 cm dan 8 cm, sehingga luas belah ketupat adalah 20 cm. Contoh ini membantu kita memahami bagaimana menghitung luas belah ketupat dalam aplikasi praktis.
Menghitung luas belah ketupat sangat penting dalam berbagai bidang seperti arsitektur, teknik, dan desain. Arsitek menggunakannya untuk menentukan luas ruangan dan merencanakan tata letak bangunan. Insinyur menggunakannya untuk menghitung luas permukaan struktur dan menentukan kebutuhan material. Desainer menggunakannya untuk membuat pola dekoratif dan karya seni yang harmonis.
Memahami cara menghitung luas belah ketupat sangat penting untuk berbagai profesi dan kegiatan sehari-hari. Contoh yang diberikan menunjukkan bagaimana konsep ini diterapkan dalam situasi nyata, sehingga memberikan wawasan tentang pentingnya dan penerapan praktisnya.
Pertanyaan Umum Seputar Luas Belah Ketupat
Berikut adalah beberapa pertanyaan umum beserta jawabannya terkait luas belah ketupat:
Pertanyaan 1: Bagaimana cara menghitung luas belah ketupat?
Luas belah ketupat dapat dihitung menggunakan rumus L = x d1 x d2, di mana d1 dan d2 adalah panjang kedua diagonal belah ketupat.
Pertanyaan 2: Apa saja aplikasi luas belah ketupat dalam kehidupan nyata?
Luas belah ketupat memiliki berbagai aplikasi dalam bidang arsitektur, teknik, dan desain. Dalam arsitektur, digunakan untuk menentukan luas ruangan dan merencanakan tata letak bangunan. Dalam teknik, digunakan untuk menghitung luas permukaan struktur dan menentukan kebutuhan material. Dalam desain, digunakan untuk membuat pola dekoratif dan karya seni yang harmonis.
Pertanyaan 3: Apakah luas belah ketupat berubah jika bentuknya diubah?
Tidak, luas belah ketupat tidak berubah jika bentuknya diubah, selama diagonalnya tetap sama panjang.
Pertanyaan 4: Siapa yang pertama kali menemukan rumus luas belah ketupat?
Rumus luas belah ketupat pertama kali ditemukan oleh matematikawan Yunani, Euclid, sekitar tahun 300 SM.
Dengan memahami jawaban atas pertanyaan-pertanyaan umum ini, kita dapat memperoleh pemahaman yang lebih baik tentang konsep luas belah ketupat dan penerapannya dalam berbagai bidang.
Artikel selengkapnya tentang tips menghitung dan menerapkan luas belah ketupat dapat ditemukan di bagian selanjutnya.
Tips Menghitung dan Menerapkan Luas Belah Ketupat
Untuk menghitung dan menerapkan luas belah ketupat secara efektif, berikut adalah beberapa tips yang dapat membantu:
Tip 1: Pastikan Diagonal Diketahui
Menghitung luas belah ketupat memerlukan panjang kedua diagonalnya. Pastikan Anda memiliki informasi ini sebelum memulai perhitungan.
Tip 2: Gunakan Rumus yang Tepat
Rumus untuk menghitung luas belah ketupat adalah L = x d1 x d2, di mana d1 dan d2 adalah panjang kedua diagonal. Gunakan rumus ini untuk mendapatkan hasil yang akurat.
Tip 3: Perhatikan Satuan
Hasil luas belah ketupat harus dinyatakan dalam satuan luas yang sesuai, seperti sentimeter persegi (cm2) atau meter persegi (m2). Pastikan untuk menyertakan satuan dalam hasil Anda.
Tip 4: Terapkan pada Aplikasi Praktis
Luas belah ketupat memiliki berbagai aplikasi dalam bidang arsitektur, teknik, dan desain. Pahami penerapan luas belah ketupat dalam konteks dunia nyata.
Dengan mengikuti tips ini, Anda dapat menghitung dan menerapkan luas belah ketupat secara akurat dan efektif.
Artikel selanjutnya akan mengulas secara mendalam tentang rumus luas belah ketupat, sifat-sifatnya, dan penerapannya dalam berbagai bidang.
Kesimpulan
Luas belah ketupat merupakan konsep penting dalam geometri dengan berbagai aplikasi praktis. Artikel ini telah mengeksplorasi konsep ini secara mendalam, menguraikan rumus untuk menghitung luas belah ketupat, sifat-sifatnya, dan penerapannya dalam bidang arsitektur, teknik, dan desain.
Memahami luas belah ketupat sangat penting bagi siapa saja yang bekerja di bidang terkait atau tertarik dengan geometri. Dengan memahami konsep ini, kita dapat memperoleh wawasan tentang bentuk geometris, pengukuran luas, dan aplikasi praktis dalam berbagai aspek kehidupan.




