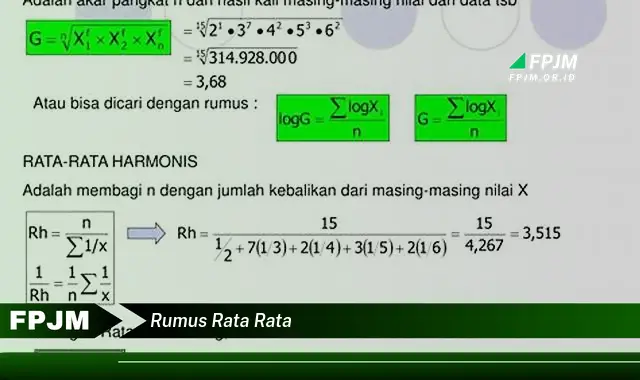
Rumus rata-rata adalah sebuah metode matematika yang digunakan untuk menghitung nilai rata-rata dari sekumpulan data. Rumus ini dihitung dengan menjumlahkan semua nilai data dan kemudian membaginya dengan jumlah data tersebut.
Rumus rata-rata sangat penting dalam berbagai bidang, seperti statistik, keuangan, dan sains. Rumus ini dapat digunakan untuk membandingkan kinerja, mengevaluasi tren, dan membuat keputusan yang tepat.
Pada artikel ini, kita akan membahas secara mendalam tentang rumus rata-rata, termasuk cara menghitungnya, jenis-jenisnya, dan penerapannya dalam kehidupan sehari-hari.
Rumus Rata-rata
Rumus rata-rata adalah metode matematika yang penting dalam berbagai bidang, seperti statistik, keuangan, dan sains. Rumus ini digunakan untuk menghitung nilai rata-rata dari sekumpulan data.
- Definisi
- Jenis
- Penghitungan
- Aplikasi
- Interpretasi
- Keterbatasan
- Alternatif
Beberapa aspek penting dari rumus rata-rata meliputi definisinya sebagai metode penghitungan nilai rata-rata, jenis-jenisnya yang berbeda (seperti mean, median, dan modus), cara penghitungannya, dan penerapannya dalam berbagai bidang. Penting juga untuk memahami interpretasi hasil perhitungan rata-rata, serta keterbatasan dan alternatif metode yang ada. Dengan memahami aspek-aspek ini, kita dapat menggunakan rumus rata-rata secara efektif untuk memperoleh informasi yang berharga dari sekumpulan data.
Definisi
Definisi rumus rata-rata sangat penting untuk memahami konsep dasar dan penggunaannya. Rumus rata-rata didefinisikan sebagai sebuah metode matematika yang digunakan untuk menghitung nilai rata-rata dari sekumpulan data. Nilai rata-rata adalah nilai yang mewakili kecenderungan sentral dari data, sehingga memberikan gambaran umum tentang distribusi data.
-
Komponen Utama Definisi
Definisi rumus rata-rata terdiri dari beberapa komponen utama, yaitu:
- Sekumpulan data: Kumpulan nilai yang akan dihitung rata-ratanya.
- Penjumlahan nilai data: Proses menjumlahkan semua nilai dalam kumpulan data.
- Pembagian dengan jumlah data: Proses membagi hasil penjumlahan dengan jumlah nilai dalam kumpulan data.
-
Jenis-Jenis Rumus Rata-rata
Terdapat beberapa jenis rumus rata-rata, antara lain:
- Rata-rata hitung (mean): Jumlah semua nilai data dibagi dengan jumlah data.
- Rata-rata median: Nilai tengah dari sekumpulan data yang telah diurutkan.
- Rata-rata modus: Nilai yang paling sering muncul dalam sekumpulan data.
-
Penerapan dalam Kehidupan Nyata
Rumus rata-rata memiliki banyak penerapan dalam kehidupan nyata, antara lain:
- Statistik: Untuk menganalisis data dan menarik kesimpulan.
- Keuangan: Untuk menghitung rata-rata keuntungan atau kerugian.
- Sains: Untuk menganalisis data eksperimen dan menarik kesimpulan.
Dengan memahami definisi rumus rata-rata, kita dapat menggunakannya secara efektif untuk memperoleh informasi yang berharga dari sekumpulan data.
Jenis
Jenis-jenis rumus rata-rata sangat penting untuk dipahami karena mempengaruhi cara perhitungan dan interpretasi hasil. Terdapat tiga jenis utama rumus rata-rata, yaitu rata-rata hitung (mean), rata-rata median, dan rata-rata modus.
Rata-rata hitung merupakan jenis yang paling umum digunakan dan dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Rata-rata median adalah nilai tengah dari sekumpulan data yang telah diurutkan, sedangkan rata-rata modus adalah nilai yang paling sering muncul dalam sekumpulan data.
Pemilihan jenis rumus rata-rata yang tepat bergantung pada jenis data dan tujuan perhitungan. Misalnya, rata-rata hitung cocok untuk data yang berdistribusi normal, sedangkan rata-rata median lebih sesuai untuk data yang memiliki nilai ekstrem atau pencilan (outlier). Memahami jenis-jenis rumus rata-rata dan penggunaannya sangat penting untuk mendapatkan hasil perhitungan yang akurat dan bermakna.
Penghitungan
Penghitungan merupakan komponen penting dalam rumus rata-rata. Tanpa penghitungan, kita tidak dapat memperoleh nilai rata-rata dari sekumpulan data.
Proses penghitungan rumus rata-rata bervariasi tergantung pada jenis rata-rata yang digunakan. Untuk rata-rata hitung, penghitungan dilakukan dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Sedangkan untuk rata-rata median, penghitungan dilakukan dengan mengurutkan data dari terkecil ke terbesar dan mengambil nilai tengah. Sementara itu, untuk rata-rata modus, penghitungan dilakukan dengan mencari nilai yang paling sering muncul.
Kemampuan menghitung rumus rata-rata dengan benar sangat penting dalam berbagai bidang, seperti statistik, keuangan, dan sains. Dengan memahami cara penghitungannya, kita dapat memperoleh informasi yang berharga dari sekumpulan data dan membuat keputusan yang tepat.
Aplikasi
Rumus rata-rata memiliki berbagai aplikasi penting dalam kehidupan nyata. Berikut adalah beberapa contohnya:
-
Statistik
Dalam statistik, rumus rata-rata digunakan untuk menganalisis data dan menarik kesimpulan. Misalnya, rata-rata penghasilan dapat digunakan untuk mengukur tingkat kesejahteraan suatu masyarakat.
-
Keuangan
Dalam keuangan, rumus rata-rata digunakan untuk menghitung rata-rata keuntungan atau kerugian. Misalnya, rata-rata pengembalian investasi dapat digunakan untuk mengevaluasi kinerja portofolio.
-
Sains
Dalam sains, rumus rata-rata digunakan untuk menganalisis data eksperimen dan menarik kesimpulan. Misalnya, rata-rata suhu dapat digunakan untuk mengukur tren perubahan iklim.
-
Pendidikan
Dalam pendidikan, rumus rata-rata digunakan untuk menghitung nilai rata-rata siswa. Misalnya, rata-rata nilai ujian dapat digunakan untuk menilai prestasi siswa.
Aplikasi rumus rata-rata tidak terbatas pada bidang-bidang tersebut saja, tetapi juga meluas ke berbagai bidang lainnya. Dengan memahami rumus rata-rata dan cara menggunakannya, kita dapat memperoleh informasi yang berharga dari sekumpulan data dan membuat keputusan yang tepat.
Interpretasi
Interpretasi hasil perhitungan rumus rata-rata merupakan langkah penting untuk memperoleh informasi yang berharga dari sekumpulan data. Interpretasi yang tepat akan membantu kita memahami makna di balik angka-angka rata-rata dan membuat keputusan yang tepat.
Dalam melakukan interpretasi, perlu mempertimbangkan beberapa hal, seperti jenis rumus rata-rata yang digunakan, distribusi data, dan konteks penggunaan. Misalnya, jika kita menggunakan rata-rata hitung untuk menghitung rata-rata penghasilan, kita perlu mempertimbangkan apakah data penghasilan terdistribusi normal atau terdapat nilai ekstrem yang dapat mempengaruhi hasil perhitungan.
Interpretasi hasil perhitungan rumus rata-rata sangat penting dalam berbagai bidang. Misalnya, dalam statistik, interpretasi rata-rata dapat membantu kita memahami tren dan pola data. Dalam keuangan, interpretasi rata-rata dapat membantu kita mengevaluasi kinerja investasi. Dalam sains, interpretasi rata-rata dapat membantu kita menarik kesimpulan dari eksperimen.
Dengan memahami cara menginterpretasikan hasil perhitungan rumus rata-rata, kita dapat memperoleh manfaat yang maksimal dari data yang kita miliki dan membuat keputusan yang tepat berdasarkan informasi yang akurat.
Keterbatasan
Rumus rata-rata, meskipun merupakan alat yang ampuh untuk merangkum data, memiliki keterbatasan tertentu yang perlu dipertimbangkan ketika menafsirkan hasil. Berikut adalah beberapa keterbatasan utama:
-
Sensitivitas terhadap nilai ekstrem
Rumus rata-rata sangat sensitif terhadap nilai ekstrem, yang dapat mendistorsi hasil. Misalnya, jika satu nilai data jauh lebih besar atau lebih kecil dari nilai lainnya, hal ini dapat secara signifikan memengaruhi nilai rata-rata.
-
Tidak mempertimbangkan distribusi data
Rumus rata-rata tidak mempertimbangkan distribusi data. Artinya, rumus rata-rata tidak dapat memberikan informasi tentang bagaimana data tersebar di sekitar nilai rata-rata.
-
Tidak memberikan informasi tentang variasi data
Rumus rata-rata hanya memberikan informasi tentang nilai rata-rata, tetapi tidak memberikan informasi tentang variasi data. Artinya, rumus rata-rata tidak dapat menunjukkan seberapa tersebar data di sekitar nilai rata-rata.
-
Tidak cocok untuk data kategorikal
Rumus rata-rata tidak cocok untuk data kategorikal, yaitu data yang tidak dapat diukur secara numerik. Misalnya, rumus rata-rata tidak dapat digunakan untuk menghitung rata-rata warna mata atau jenis kelamin.
Dengan memahami keterbatasan ini, kita dapat menggunakan rumus rata-rata secara efektif dan menghindari kesalahan interpretasi. Selain itu, kita dapat mempertimbangkan menggunakan ukuran statistik lain yang lebih tepat untuk mengatasi keterbatasan rumus rata-rata.
Alternatif
Dalam konteks rumus rata-rata, alternatif merujuk pada metode atau ukuran statistik lain yang dapat digunakan untuk meringkas data selain rumus rata-rata. Alternatif ini dapat mengatasi keterbatasan rumus rata-rata dan memberikan informasi tambahan tentang data.
-
Median
Median adalah nilai tengah dari sekumpulan data yang telah diurutkan. Median tidak sensitif terhadap nilai ekstrem dan memberikan gambaran yang lebih baik tentang nilai tipikal dalam data dibandingkan rata-rata hitung.
-
Modus
Modus adalah nilai yang paling sering muncul dalam sekumpulan data. Modus berguna untuk mengidentifikasi nilai yang paling umum atau dominan dalam data.
-
Jangkauan
Jangkauan adalah selisih antara nilai maksimum dan minimum dalam sekumpulan data. Jangkauan memberikan informasi tentang variasi data.
-
Simpangan Baku
Simpangan baku adalah ukuran statistik yang mengukur seberapa tersebar data di sekitar nilai rata-rata. Simpangan baku berguna untuk mengidentifikasi data yang sangat bervariasi atau memiliki nilai ekstrem.
Pemilihan alternatif yang tepat bergantung pada jenis data, tujuan analisis, dan keterbatasan rumus rata-rata. Dengan memahami alternatif yang tersedia, kita dapat memilih ukuran statistik yang paling tepat untuk memperoleh informasi yang berharga dari data.
Pertanyaan Umum tentang Rumus Rata-rata
Berikut adalah beberapa pertanyaan umum dan jawabannya tentang rumus rata-rata:
Pertanyaan 1: Apa itu rumus rata-rata?
Rumus rata-rata adalah metode matematika yang digunakan untuk menghitung nilai rata-rata dari sekumpulan data. Nilai rata-rata adalah nilai yang mewakili kecenderungan sentral dari data.
Pertanyaan 2: Kapan rumus rata-rata digunakan?
Rumus rata-rata digunakan dalam berbagai bidang, seperti statistik, keuangan, dan sains, untuk menganalisis data dan membuat kesimpulan.
Pertanyaan 3: Apa saja jenis-jenis rumus rata-rata?
Jenis-jenis rumus rata-rata yang umum digunakan meliputi rata-rata hitung (mean), rata-rata median, dan rata-rata modus.
Pertanyaan 4: Bagaimana cara menghitung rumus rata-rata?
Cara menghitung rumus rata-rata tergantung pada jenis rata-rata yang digunakan. Untuk rata-rata hitung, rumusnya adalah jumlah semua nilai data dibagi dengan jumlah data.
Kesimpulan:Rumus rata-rata adalah alat yang penting untuk menganalisis data dan memperoleh informasi yang berharga. Dengan memahami konsep dan cara menggunakan rumus rata-rata, kita dapat membuat keputusan yang tepat berdasarkan data yang tersedia.
Tips:Untuk menggunakan rumus rata-rata secara efektif, pertimbangkan jenis data, tujuan analisis, dan keterbatasan rumus rata-rata. Selain itu, pertimbangkan untuk menggunakan alternatif rumus rata-rata untuk mendapatkan informasi yang lebih komprehensif tentang data.
Tips Menggunakan Rumus Rata-rata
Untuk menggunakan rumus rata-rata secara efektif, pertimbangkan hal-hal berikut:
Tip 1: Pahami jenis data
Jenis data yang kamu miliki akan menentukan jenis rumus rata-rata yang tepat untuk digunakan. Misalnya, jika data kamu berdistribusi normal, maka rata-rata hitung (mean) dapat digunakan. Jika terdapat nilai ekstrem, maka median atau modus mungkin lebih sesuai.
Tip 2: Tentukan tujuan analisis
Tujuan kamu melakukan analisis data akan memengaruhi pilihan rumus rata-rata. Jika kamu ingin mengetahui nilai rata-rata secara keseluruhan, maka rata-rata hitung dapat digunakan. Jika kamu ingin mengetahui nilai yang paling umum, maka modus dapat menjadi pilihan yang tepat.
Tip 3: Pertimbangkan keterbatasan rumus rata-rata
Rumus rata-rata memiliki keterbatasan, seperti sensitivitas terhadap nilai ekstrem dan ketidakmampuan untuk mempertimbangkan distribusi data. Dengan memahami keterbatasan ini, kamu dapat memilih metode alternatif yang lebih sesuai untuk data kamu.
Tip 4: Gunakan alternatif rumus rata-rata
Selain rumus rata-rata hitung, median, dan modus, terdapat beberapa ukuran statistik alternatif yang dapat digunakan untuk meringkas data, seperti jangkauan dan simpangan baku. Pemilihan alternatif yang tepat bergantung pada jenis data dan tujuan analisis.
Kesimpulan:Dengan mengikuti tips ini, kamu dapat menggunakan rumus rata-rata secara efektif untuk mendapatkan informasi yang berharga dari data kamu. Memahami jenis data, menentukan tujuan analisis, mempertimbangkan keterbatasan, dan menggunakan alternatif yang sesuai akan membantu kamu membuat keputusan yang tepat berdasarkan data yang kamu miliki.
Kesimpulan
Rumus rata-rata merupakan alat penting dalam berbagai bidang untuk meringkas data dan memperoleh informasi yang berharga. Dengan memahami konsep, jenis, penghitungan, aplikasi, interpretasi, keterbatasan, dan alternatifnya, kita dapat menggunakan rumus rata-rata secara efektif untuk membuat keputusan yang tepat.
Dalam menggunakan rumus rata-rata, penting untuk mempertimbangkan jenis data, tujuan analisis, dan keterbatasannya. Selain itu, kita dapat menggunakan alternatif rumus rata-rata untuk mendapatkan informasi yang lebih komprehensif tentang data. Dengan demikian, kita dapat memaksimalkan manfaat rumus rata-rata dan memperoleh wawasan yang berharga dari data yang kita miliki.




