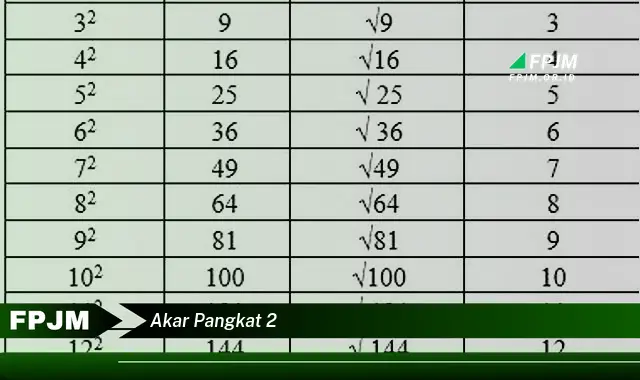
Akar pangkat dua, juga dikenal sebagai akar kuadrat, adalah operasi matematika yang menghasilkan bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli. Misalnya, akar pangkat dua dari 9 adalah 3, karena 3 x 3 = 9.
Akar pangkat dua memiliki banyak aplikasi penting dalam kehidupan nyata, seperti menghitung panjang sisi segitiga siku-siku, menentukan luas lingkaran, dan menyelesaikan persamaan kuadrat. Konsep akar pangkat dua juga telah memainkan peran penting dalam perkembangan matematika selama berabad-abad.
Artikel ini akan membahas dasar-dasar akar pangkat dua, termasuk definisi, sifat, dan aplikasinya. Kami juga akan mengeksplorasi sejarah akar pangkat dua dan peran pentingnya dalam matematika.
Akar Pangkat Dua
Akar pangkat dua, meskipun merupakan konsep matematika yang sederhana, memiliki banyak aspek penting yang membuatnya sangat berguna dan penting dalam berbagai bidang.
- Definisi
- Sifat
- Aplikasi
- Sejarah
- Geometri
- Trigonometri
- Persamaan
Definisi akar pangkat dua sebagai operasi yang menghasilkan bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli, membuatnya menjadi dasar bagi banyak konsep matematika lainnya. Sifat-sifat akar pangkat dua, seperti sifat distributif dan asosiatif, menjadikannya mudah untuk dimanipulasi dan diterapkan dalam berbagai situasi. Aplikasi akar pangkat dua sangat luas, mulai dari menghitung panjang sisi segitiga siku-siku hingga menyelesaikan persamaan kuadrat. Sejarah akar pangkat dua menunjukkan perkembangan konsep ini selama berabad-abad, dari akar kuadrat pada zaman Babilonia hingga pengembangan notasi modern pada abad pertengahan. Dalam geometri, akar pangkat dua digunakan untuk menghitung jarak, luas, dan volume bangun ruang. Dalam trigonometri, akar pangkat dua digunakan untuk menyelesaikan persamaan trigonometri dan menghitung nilai fungsi trigonometri. Dalam persamaan, akar pangkat dua digunakan untuk menyelesaikan persamaan kuadrat dan persamaan lainnya yang melibatkan eksponen kuadrat.
Definisi
Definisi akar pangkat dua merupakan dasar dari pemahaman kita tentang operasi matematika penting ini. Akar pangkat dua suatu bilangan didefinisikan sebagai bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli. Misalnya, akar pangkat dua dari 9 adalah 3, karena 3 x 3 = 9.
-
Konsep Dasar
Konsep akar pangkat dua sangat penting dalam matematika. Akar pangkat dua digunakan dalam berbagai aplikasi, seperti menghitung panjang sisi segitiga siku-siku, menentukan luas lingkaran, dan menyelesaikan persamaan kuadrat.
Definisi akar pangkat dua memberikan dasar yang kuat untuk memahami sifat-sifat dan aplikasi operasi matematika penting ini.
Sifat
Sifat-sifat akar pangkat dua sangat penting untuk dipahami karena sifat-sifat ini memungkinkan kita untuk memanipulasi dan menggunakan akar pangkat dua secara efektif dalam berbagai situasi. Sifat-sifat ini meliputi:
- Sifat Distributif: Akar pangkat dua dari jumlah dua bilangan kuadrat sama dengan jumlah akar pangkat dua dari masing-masing bilangan tersebut.
- Sifat Asosiatif: Akar pangkat dua dari hasil kali dua bilangan kuadrat sama dengan hasil kali akar pangkat dua dari masing-masing bilangan tersebut.
- Sifat Perpangkatan: Akar pangkat dua dari suatu bilangan yang dipangkatkan suatu bilangan bulat positif sama dengan pangkat setengah dari bilangan tersebut.
Sifat-sifat ini sangat berguna dalam menyelesaikan berbagai masalah matematika. Misalnya, sifat distributif dapat digunakan untuk menyederhanakan ekspresi yang melibatkan akar pangkat dua, sementara sifat asosiatif dapat digunakan untuk mengelompokkan suku-suku serupa. Sifat perpangkatan dapat digunakan untuk menyederhanakan ekspresi yang melibatkan bilangan berpangkat.
Memahami sifat-sifat akar pangkat dua sangat penting untuk menggunakan operasi matematika ini secara efektif. Sifat-sifat ini memungkinkan kita untuk memanipulasi dan menggunakan akar pangkat dua dengan cara yang efisien dan akurat.
Aplikasi
Akar pangkat dua memiliki banyak aplikasi dalam berbagai bidang, seperti matematika, fisika, teknik, dan keuangan. Salah satu aplikasi yang paling umum adalah untuk menghitung panjang sisi segitiga siku-siku menggunakan teorema Pythagoras. Aplikasi penting lainnya adalah untuk menyelesaikan persamaan kuadrat, yang muncul dalam berbagai masalah dunia nyata, seperti menghitung lintasan proyektil atau menentukan titik potong grafik.
Dalam fisika, akar pangkat dua digunakan untuk menghitung kecepatan, percepatan, dan gaya. Dalam teknik, akar pangkat dua digunakan untuk menghitung tegangan, arus, dan daya dalam rangkaian listrik. Dalam keuangan, akar pangkat dua digunakan untuk menghitung suku bunga, pengembalian investasi, dan nilai waktu uang.
Memahami aplikasi akar pangkat dua sangat penting untuk memecahkan berbagai masalah dalam kehidupan nyata. Aplikasi-aplikasi ini menunjukkan pentingnya akar pangkat dua sebagai alat matematika yang ampuh dan serbaguna.
Sejarah
Sejarah akar pangkat dua berawal dari zaman kuno, ketika matematikawan Babilonia mengembangkan metode untuk menghitung akar kuadrat menggunakan tabel dan algoritma. Konsep akar pangkat dua kemudian disempurnakan oleh matematikawan Yunani, seperti Pythagoras dan Euclid, yang mengembangkan metode geometris untuk menghitung akar kuadrat.
-
Pengaruh Matematikawan Yunani
Matematikawan Yunani, seperti Pythagoras dan Euclid, memainkan peran penting dalam perkembangan akar pangkat dua. Mereka mengembangkan metode geometris untuk menghitung akar kuadrat, yang memberikan dasar bagi metode yang digunakan hingga sekarang.
-
Penggunaan dalam Arsitektur dan Seni
Akar pangkat dua juga digunakan dalam arsitektur dan seni pada zaman kuno. Arsitek Yunani menggunakan akar pangkat dua untuk menghitung proporsi bangunan, sementara seniman Yunani menggunakannya untuk menciptakan ilusi kedalaman dan perspektif dalam karya seni mereka.
-
Perkembangan Notasi Modern
Notasi modern untuk akar pangkat dua, yaitu simbol , dikembangkan pada abad pertengahan oleh matematikawan India dan Arab. Notasi ini menyederhanakan perhitungan akar pangkat dua dan membuatnya lebih mudah untuk digunakan dalam persamaan dan ekspresi matematika.
-
Penggunaan dalam Matematika Modern
Akar pangkat dua terus memainkan peran penting dalam matematika modern. Akar pangkat dua digunakan dalam berbagai bidang matematika, termasuk aljabar, kalkulus, dan geometri.
Sejarah akar pangkat dua mencerminkan pentingnya konsep ini dalam matematika dan aplikasinya yang luas di berbagai bidang. Dari metode kuno untuk menghitung akar kuadrat hingga notasi modern yang digunakan saat ini, akar pangkat dua telah memainkan peran penting dalam perkembangan matematika dan terus menjadi konsep dasar yang penting dalam matematika modern.
Geometri
Akar pangkat dua memiliki peran penting dalam geometri, terutama dalam menghitung panjang sisi, luas, dan volume bangun ruang. Konsep akar pangkat dua digunakan dalam berbagai aplikasi geometri, seperti:
-
Menghitung Panjang Sisi Segitiga Siku-siku
Akar pangkat dua digunakan untuk menghitung panjang sisi miring segitiga siku-siku menggunakan teorema Pythagoras. Teorema ini menyatakan bahwa kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya.
-
Menghitung Luas Lingkaran
Akar pangkat dua digunakan untuk menghitung luas lingkaran menggunakan rumus . Rumus ini menyatakan bahwa luas lingkaran sama dengan kuadrat dari jari-jari dikalikan dengan .
-
Menghitung Volume Kubus dan Balok
Akar pangkat dua digunakan untuk menghitung volume kubus dan balok menggunakan rumus . Rumus ini menyatakan bahwa volume kubus atau balok sama dengan panjang dikalikan lebar dikalikan tinggi.
-
Menghitung Jarak Titik ke Garis
Akar pangkat dua digunakan untuk menghitung jarak titik ke garis menggunakan rumus . Rumus ini menyatakan bahwa jarak titik ke garis sama dengan panjang garis dari titik ke garis dibagi dengan panjang garis.
Akar pangkat dua merupakan konsep dasar dalam geometri yang digunakan untuk menyelesaikan berbagai masalah. Pemahaman tentang akar pangkat dua sangat penting untuk memahami dan menerapkan konsep-konsep geometri secara efektif.
Trigonometri
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Akar pangkat dua memainkan peran penting dalam trigonometri, terutama dalam menghitung nilai fungsi trigonometri dan menyelesaikan persamaan trigonometri.
-
Menghitung Nilai Fungsi Trigonometri
Akar pangkat dua digunakan untuk menghitung nilai fungsi sinus, kosinus, dan tangen menggunakan definisi fungsi trigonometri. Definisi ini melibatkan perbandingan panjang sisi segitiga siku-siku, yang dapat dihitung menggunakan teorema Pythagoras dan akar pangkat dua.
-
Menyelesaikan Persamaan Trigonometri
Akar pangkat dua juga digunakan untuk menyelesaikan persamaan trigonometri, seperti persamaan yang melibatkan fungsi sinus, kosinus, atau tangen. Persamaan trigonometri ini dapat dimodifikasi untuk mengisolasi sudut yang tidak diketahui, yang dapat dihitung menggunakan akar pangkat dua.
-
Menghitung Sudut Elevasi dan Depresi
Akar pangkat dua digunakan dalam trigonometri untuk menghitung sudut elevasi dan depresi. Sudut elevasi adalah sudut antara garis horizontal dan garis yang menghubungkan pengamat ke objek yang lebih tinggi. Sudut depresi adalah sudut antara garis horizontal dan garis yang menghubungkan pengamat ke objek yang lebih rendah. Kedua sudut ini dapat dihitung menggunakan akar pangkat dua dan prinsip-prinsip trigonometri.
-
Menghitung Jarak Menggunakan Trigonometri
Akar pangkat dua juga digunakan dalam trigonometri untuk menghitung jarak antara dua titik yang tidak dapat diukur secara langsung. Metode ini melibatkan penggunaan fungsi trigonometri dan prinsip-prinsip geometri, dan dapat digunakan untuk menghitung jarak ke objek yang jauh, seperti bintang atau puncak gunung.
Pemahaman tentang akar pangkat dua sangat penting untuk memahami dan menerapkan konsep-konsep trigonometri secara efektif. Akar pangkat dua memungkinkan kita untuk menghitung nilai fungsi trigonometri, menyelesaikan persamaan trigonometri, dan menghitung sudut dan jarak menggunakan prinsip-prinsip trigonometri.
Persamaan
Persamaan adalah pernyataan matematika yang menyatakan bahwa dua ekspresi memiliki nilai yang sama. Akar pangkat dua memainkan peran penting dalam menyelesaikan banyak jenis persamaan, terutama persamaan kuadrat.
-
Menyelesaikan Persamaan Kuadrat
Salah satu aplikasi paling umum dari akar pangkat dua adalah dalam menyelesaikan persamaan kuadrat, yaitu persamaan yang berbentuk ax + bx + c = 0, di mana a, b, dan c adalah konstanta. Akar pangkat dua digunakan untuk menemukan nilai x yang memenuhi persamaan tersebut.
Dengan memahami peran akar pangkat dua dalam menyelesaikan persamaan, kita dapat menggunakan konsep ini untuk memecahkan berbagai masalah matematika dan aplikasi di dunia nyata yang melibatkan persamaan kuadrat.
Pertanyaan Umum tentang Akar Pangkat Dua
Bagian ini akan membahas beberapa pertanyaan umum yang sering diajukan tentang akar pangkat dua.
Pertanyaan 1: Apa yang dimaksud dengan akar pangkat dua?
Akar pangkat dua suatu bilangan adalah bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli tersebut.
Pertanyaan 2: Bagaimana cara menghitung akar pangkat dua?
Ada beberapa metode untuk menghitung akar pangkat dua, termasuk menggunakan kalkulator, tabel, atau algoritma pembagian panjang.
Pertanyaan 3: Apa saja sifat-sifat akar pangkat dua?
Akar pangkat dua memiliki beberapa sifat penting, seperti sifat distributif, asosiatif, dan perpangkatan.
Pertanyaan 4: Bagaimana akar pangkat dua digunakan dalam kehidupan nyata?
Akar pangkat dua memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung panjang sisi segitiga siku-siku, menentukan luas lingkaran, dan menyelesaikan persamaan kuadrat.
Dengan memahami dasar-dasar akar pangkat dua, kita dapat menggunakan konsep ini untuk memecahkan berbagai masalah matematika dan aplikasi di dunia nyata.
Beralih ke bagian Tips untuk mempelajari cara menggunakan akar pangkat dua secara efektif.
Tips Mempelajari Akar Pangkat Dua
Beberapa tips berikut dapat membantu Anda memahami dan menggunakan akar pangkat dua secara efektif:
Tip 1: Pahami Konsep Dasar
Langkah pertama untuk menguasai akar pangkat dua adalah memahami konsep dasarnya. Pastikan Anda memahami definisi akar pangkat dua dan sifat-sifatnya, seperti sifat distributif dan asosiatif.
Tip 2: Latihan Soal Sederhana
Cara terbaik untuk meningkatkan keterampilan Anda dalam akar pangkat dua adalah dengan berlatih soal-soal sederhana. Mulailah dengan soal-soal dasar seperti mencari akar pangkat dua dari bilangan kuadrat sempurna. Seiring waktu, Anda dapat beralih ke soal-soal yang lebih kompleks.
Tip 3: Gunakan Kalkulator atau Tabel
Kalkulator atau tabel dapat menjadi alat yang berguna saat Anda belajar akar pangkat dua. Kalkulator dapat menghitung akar pangkat dua dengan cepat dan akurat, sementara tabel dapat memberikan perkiraan nilai akar pangkat dua.
Tip 4: Terapkan dalam Masalah Dunia Nyata
Salah satu cara terbaik untuk memahami pentingnya akar pangkat dua adalah dengan menerapkannya dalam masalah dunia nyata. Cobalah gunakan akar pangkat dua untuk menghitung panjang sisi segitiga siku-siku atau menentukan luas lingkaran.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang akar pangkat dua dan menggunakannya secara efektif untuk menyelesaikan berbagai masalah matematika dan aplikasi di dunia nyata.
Kesimpulannya, akar pangkat dua merupakan konsep matematika penting yang memiliki banyak aplikasi dalam berbagai bidang. Dengan memahami konsep dasar, berlatih soal-soal, dan menerapkannya dalam masalah dunia nyata, Anda dapat menguasai akar pangkat dua dan menggunakannya untuk memecahkan berbagai masalah secara efektif.
Akar pangkat dua merupakan konsep matematika fundamental yang banyak diaplikasikan dalam berbagai bidang. Dengan memahami konsep dasarnya, melatih soal-soal, dan mengimplementasikannya dalam konteks dunia nyata, kita dapat menguasai akar pangkat dua dan memanfaatkannya untuk menyelesaikan berbagai permasalahan secara efektif.
Penguasaan akar pangkat dua tidak hanya penting untuk kesuksesan akademis dalam matematika, tetapi juga memiliki signifikansi praktis dalam kehidupan sehari-hari. Dari menghitung panjang sisi segitiga siku-siku hingga menentukan luas lingkaran, akar pangkat dua berperan penting dalam berbagai aplikasi yang kita jumpai.
Dengan terus mengeksplorasi dan mengaplikasikan akar pangkat dua, kita dapat semakin menghargai keindahan dan kekuatan matematika, serta memanfaatkannya untuk memajukan pemahaman kita tentang dunia di sekitar kita.




