Akar pangkat 3 atau yang biasa disebut dengan kubus adalah operasi matematika yang merupakan kebalikan dari perpangkatan tiga. Jika a = b, maka akar pangkat 3 dari b adalah a. Misalnya, akar pangkat 3 dari 27 adalah 3 karena 3 = 27.
Akar pangkat 3 memiliki banyak kegunaan dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, akar pangkat 3 digunakan untuk menyelesaikan persamaan kubik dan polinomial lainnya. Dalam fisika, akar pangkat 3 digunakan untuk menghitung volume benda dan jarak tempuh benda yang bergerak dengan percepatan tetap. Dalam teknik, akar pangkat 3 digunakan untuk menghitung momen inersia dan momen gaya.
Konsep akar pangkat 3 telah dikenal sejak zaman kuno. Matematikawan Yunani Archimedes mengembangkan metode untuk menghitung akar pangkat 3 menggunakan poligon beraturan. Metode ini kemudian disempurnakan oleh matematikawan India pada abad ke-12 dan matematikawan Persia pada abad ke-15. Pada abad ke-16, matematikawan Italia Gerolamo Cardano mengembangkan rumus untuk menyelesaikan persamaan kubik, yang melibatkan penggunaan akar pangkat 3.
Akar Pangkat 3
Akar pangkat 3 atau kubus adalah operasi matematika yang penting dengan berbagai kegunaan. Berikut adalah tujuh aspek penting terkait akar pangkat 3:
- Definisi
- Rumus
- Sifat
- Aplikasi
- Sejarah
- Contoh
- Koneksi
Definisi akar pangkat 3 adalah bilangan yang jika dipangkatkan tiga akan menghasilkan bilangan semula. Rumus akar pangkat 3 adalah a = b jika a = b. Sifat-sifat akar pangkat 3 antara lain invers dari pangkat tiga, distributif terhadap penjumlahan dan pengurangan, serta transitif. Akar pangkat 3 memiliki banyak aplikasi dalam berbagai bidang, seperti matematika, fisika, dan teknik. Sejarah perkembangan konsep akar pangkat 3 telah dikenal sejak zaman kuno dan terus berkembang hingga sekarang. Contoh penggunaan akar pangkat 3 dapat ditemukan dalam kehidupan sehari-hari, seperti menghitung volume kubus dan jarak tempuh benda yang bergerak dengan percepatan tetap. Akar pangkat 3 juga memiliki keterkaitan dengan konsep-konsep matematika lainnya, seperti limit, turunan, dan integral.
Definisi Akar Pangkat 3
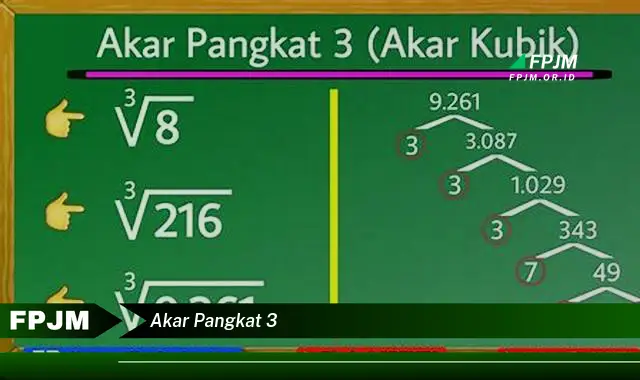
Definisi akar pangkat 3 merupakan dasar dari operasi matematika ini. Akar pangkat 3 dari suatu bilangan adalah bilangan yang jika dipangkatkan tiga akan menghasilkan bilangan semula. Misalnya, akar pangkat 3 dari 8 adalah 2 karena 2^3 = 8.
-
Sifat Dasar
Akar pangkat 3 memiliki sifat-sifat dasar, seperti invers dari pangkat tiga, distributif terhadap penjumlahan dan pengurangan, serta transitif. Sifat-sifat ini menjadi dasar penggunaan akar pangkat 3 dalam berbagai operasi matematika.
-
Notasi dan Simbol
Akar pangkat 3 biasanya dinotasikan dengan simbol pangkat tiga, yaitu . Simbol ini diletakkan di depan bilangan yang akan diakarkan. Misalnya, 8 dibaca “akar pangkat tiga dari 8”.
-
Metode Penghitungan
Ada beberapa metode untuk menghitung akar pangkat tiga, antara lain menggunakan kalkulator, tabel akar, atau algoritma perkiraan. Metode-metode ini memudahkan penyelesaian akar pangkat tiga, terutama untuk bilangan besar atau bilangan yang tidak memiliki akar pangkat tiga eksak.
-
Aplikasi dalam Kehidupan Nyata
Akar pangkat 3 memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung volume kubus, jarak tempuh benda yang bergerak dengan percepatan tetap, dan menentukan konsentrasi larutan kimia. Pemahaman tentang definisi dan sifat akar pangkat 3 sangat penting untuk menyelesaikan masalah-masalah ini.
Dengan memahami definisi dan sifat dasar akar pangkat 3, kita dapat mengaplikasikannya dalam berbagai bidang matematika dan kehidupan nyata. Definisi ini menjadi dasar untuk memahami konsep akar pangkat tiga yang lebih kompleks dan penggunaannya dalam operasi matematika yang lebih luas.
Rumus
Rumus memegang peranan penting dalam operasi akar pangkat 3. Rumus dasar akar pangkat 3 adalah 3a = b jika a = b3. Rumus ini menjadi dasar untuk menghitung akar pangkat 3 dari suatu bilangan. Misalnya, untuk mencari akar pangkat 3 dari 27, kita dapat menggunakan rumus 327 = b jika 27 = b3. Dari persamaan tersebut, kita dapat menentukan bahwa b = 3 karena 33 = 27.
Selain rumus dasar, terdapat juga rumus-rumus lain yang berkaitan dengan akar pangkat 3, seperti rumus penjumlahan dan pengurangan akar pangkat 3, rumus perkalian dan pembagian akar pangkat 3, serta rumus akar pangkat 3 dari suatu pecahan. Rumus-rumus ini sangat berguna dalam menyelesaikan berbagai operasi matematika yang melibatkan akar pangkat 3.
Pemahaman tentang rumus akar pangkat 3 sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, rumus akar pangkat 3 digunakan untuk menyelesaikan persamaan kubik dan persamaan lainnya yang melibatkan akar pangkat 3. Dalam fisika, rumus akar pangkat 3 digunakan untuk menghitung volume benda dan jarak tempuh benda yang bergerak dengan percepatan tetap. Dalam teknik, rumus akar pangkat 3 digunakan untuk menghitung momen inersia dan momen gaya.
Dengan memahami rumus akar pangkat 3, kita dapat menyelesaikan berbagai masalah matematika dan fisika yang melibatkan operasi akar pangkat 3. Pemahaman ini juga penting untuk mengaplikasikan akar pangkat 3 dalam berbagai bidang praktis, seperti teknik dan arsitektur.
Sifat Akar Pangkat 3
Sifat-sifat akar pangkat 3 sangat penting untuk memahami cara kerja operasi matematika ini. Sifat-sifat ini menjelaskan perilaku akar pangkat 3 dalam berbagai operasi dan memberikan dasar untuk penggunaannya dalam menyelesaikan masalah matematika.
-
Invers dari Pangkat Tiga
Salah satu sifat penting akar pangkat 3 adalah merupakan invers dari pangkat tiga. Artinya, jika a = b3, maka akar pangkat tiga dari b adalah a. Sifat ini menjadi dasar untuk menghitung akar pangkat tiga dan menyelesaikan persamaan yang melibatkan akar pangkat tiga.
-
Distributif terhadap Penjumlahan dan Pengurangan
Akar pangkat 3 bersifat distributif terhadap penjumlahan dan pengurangan. Artinya, akar pangkat tiga dari jumlah atau selisih dua bilangan sama dengan jumlah atau selisih akar pangkat tiga dari masing-masing bilangan tersebut. Sifat ini sangat berguna dalam menyederhanakan operasi akar pangkat 3.
-
Transitif
Sifat transitif akar pangkat 3 menyatakan bahwa jika a = b3 dan b = c3, maka a = c3. Sifat ini menunjukkan hubungan keterkaitan antar akar pangkat tiga dari bilangan-bilangan yang berbeda.
-
Monotik
Akar pangkat tiga adalah fungsi monotonik, artinya jika a > b, maka akar pangkat tiga dari a lebih besar dari akar pangkat tiga dari b. Sifat ini sangat berguna dalam menyelesaikan pertidaksamaan yang melibatkan akar pangkat tiga.
Pemahaman tentang sifat-sifat akar pangkat 3 sangat penting dalam berbagai bidang matematika dan kehidupan nyata. Sifat-sifat ini menjadi dasar untuk menyelesaikan berbagai masalah yang melibatkan akar pangkat tiga dan mengaplikasikannya dalam berbagai bidang praktis.
Aplikasi
Akar pangkat tiga memiliki beragam aplikasi dalam berbagai bidang, baik teoretis maupun praktis. Salah satu aplikasi pentingnya adalah dalam bidang matematika, di mana akar pangkat tiga digunakan untuk menyelesaikan persamaan kubik dan persamaan lainnya yang melibatkan akar pangkat tiga. Selain itu, akar pangkat tiga juga digunakan dalam fisika untuk menghitung volume benda dan jarak tempuh benda yang bergerak dengan percepatan tetap.
Dalam bidang teknik, akar pangkat tiga berperan penting dalam menghitung momen inersia dan momen gaya. Misalnya, dalam rekayasa struktur, akar pangkat tiga digunakan untuk menghitung momen inersia balok dan pelat, yang penting untuk menentukan kekuatan dan stabilitas struktur tersebut. Selain itu, akar pangkat tiga juga digunakan dalam bidang kimia untuk menentukan konsentrasi larutan dan dalam bidang ekonomi untuk menghitung pertumbuhan ekonomi dan inflasi.
Pemahaman tentang aplikasi akar pangkat tiga sangat penting bagi para profesional di berbagai bidang. Dalam matematika, fisika, teknik, dan kimia, pengetahuan tentang akar pangkat tiga memungkinkan para peneliti dan praktisi untuk menyelesaikan masalah kompleks dan mengembangkan solusi inovatif. Dengan memahami aplikasi akar pangkat tiga, kita dapat memanfaatkan kekuatan matematika ini untuk memajukan pengetahuan dan memecahkan tantangan dunia nyata.
Sejarah
Sejarah memiliki hubungan yang erat dengan akar pangkat tiga. Pemahaman tentang sejarah perkembangan akar pangkat tiga membantu kita mengapresiasi konsep ini secara lebih mendalam dan memahami pentingnya dalam matematika dan bidang lainnya.
Konsep akar pangkat tiga telah dikenal sejak zaman kuno. Matematikawan Babilonia dan Mesir Kuno mengembangkan metode untuk menghitung akar pangkat tiga menggunakan tabel dan algoritma. Matematikawan Yunani seperti Archimedes dan Apollonius juga mempelajari akar pangkat tiga dan mengembangkan metode yang lebih canggih untuk menghitungnya.
Pada abad pertengahan, matematikawan Persia dan India memberikan kontribusi signifikan terhadap perkembangan konsep akar pangkat tiga. Matematikawan Persia Al-Khwarizmi mengembangkan rumus untuk menyelesaikan persamaan kubik, yang melibatkan penggunaan akar pangkat tiga. Matematikawan India seperti Brahmagupta dan Bhaskara II juga mengembangkan metode baru untuk menghitung akar pangkat tiga.
Pada abad ke-16, matematikawan Italia Gerolamo Cardano menerbitkan rumus terkenal untuk menyelesaikan persamaan kubik, yang dikenal sebagai rumus Cardano. Rumus ini didasarkan pada konsep akar pangkat tiga dan menjadi tonggak penting dalam sejarah matematika.
Pemahaman tentang sejarah akar pangkat tiga sangat penting karena beberapa alasan. Pertama, sejarah membantu kita menghargai kompleksitas dan keindahan konsep matematika ini. Kedua, sejarah menunjukkan bagaimana akar pangkat tiga telah berkembang dari waktu ke waktu dan bagaimana konsep ini telah digunakan untuk memecahkan masalah dalam berbagai bidang.
Kesimpulannya, sejarah memiliki hubungan yang erat dengan akar pangkat tiga. Pemahaman tentang sejarah perkembangan akar pangkat tiga membantu kita mengapresiasi konsep ini secara lebih mendalam, memahami pentingnya dalam matematika dan bidang lainnya, serta menghargai kontribusi para matematikawan sepanjang sejarah terhadap perkembangan konsep ini.
Contoh
Contoh memainkan peran penting dalam memahami akar pangkat 3. Contoh konkret membantu memvisualisasikan konsep abstrak dan mengilustrasikan penerapan akar pangkat 3 dalam berbagai konteks.
Salah satu contoh umum akar pangkat 3 adalah menghitung volume kubus. Volume kubus dapat dihitung menggunakan rumus V = a, di mana a adalah panjang rusuk kubus. Contoh ini menunjukkan bagaimana akar pangkat 3 digunakan untuk menentukan volume benda tiga dimensi.
Contoh lain adalah menghitung jarak tempuh benda yang bergerak dengan percepatan tetap. Rumus jarak tempuh s = vt menunjukkan bagaimana akar pangkat 3 digunakan untuk menghitung jarak yang ditempuh benda dalam selang waktu tertentu. Contoh ini menyoroti aplikasi akar pangkat 3 dalam fisika.
Selain itu, akar pangkat 3 juga digunakan dalam bidang kimia untuk menghitung konsentrasi larutan. Rumus konsentrasi C = n/V, di mana n adalah jumlah mol zat terlarut dan V adalah volume larutan, menunjukkan bagaimana akar pangkat 3 digunakan untuk menentukan konsentrasi zat dalam larutan.
Memahami hubungan antara akar pangkat 3 dan contoh-contoh ini sangat penting karena memungkinkan kita untuk melihat penerapan praktis konsep ini di berbagai bidang. Contoh-contoh ini membantu kita memahami pentingnya akar pangkat 3 dalam menyelesaikan masalah dunia nyata dan mengembangkan solusi inovatif.
Koneksi
Akar pangkat tiga memiliki keterkaitan erat dengan berbagai konsep dan bidang matematika lainnya. Koneksi-koneksi ini memperluas pemahaman kita tentang akar pangkat tiga dan menyoroti pentingnya konsep ini dalam matematika.
-
Limit dan Turunan
Akar pangkat tiga terkait erat dengan konsep limit dan turunan. Limit dari suatu fungsi yang melibatkan akar pangkat tiga dapat dievaluasi menggunakan aturan limit. Turunan dari suatu fungsi yang melibatkan akar pangkat tiga dapat dihitung menggunakan aturan rantai. Koneksi ini menunjukkan keterkaitan antara akar pangkat tiga dan kalkulus.
-
Integral
Akar pangkat tiga juga terhubung dengan integral. Integral dari suatu fungsi yang melibatkan akar pangkat tiga dapat dievaluasi menggunakan substitusi atau teknik integrasi lainnya. Koneksi ini menunjukkan keterkaitan antara akar pangkat tiga dan integral, yang merupakan dasar dari kalkulus.
-
Persamaan Diferensial
Akar pangkat tiga muncul dalam penyelesaian persamaan diferensial tertentu. Misalnya, persamaan diferensial yang melibatkan suku akar pangkat tiga dapat diselesaikan menggunakan metode pemisahan variabel. Koneksi ini menunjukkan keterkaitan antara akar pangkat tiga dan persamaan diferensial, yang digunakan untuk memodelkan berbagai fenomena fisika dan teknik.
-
Teori Bilangan
Akar pangkat tiga juga terhubung dengan teori bilangan. Misalnya, akar pangkat tiga dari bilangan bulat positif dapat digunakan untuk mengklasifikasikan bilangan bulat tersebut sebagai bilangan prima atau komposit. Koneksi ini menunjukkan keterkaitan antara akar pangkat tiga dan teori bilangan, yang mempelajari sifat-sifat bilangan bulat.
Koneksi-koneksi ini menunjukkan bahwa akar pangkat tiga tidak hanya sekadar operasi matematika yang berdiri sendiri, tetapi juga terkait erat dengan banyak konsep dan bidang matematika lainnya. Pemahaman tentang koneksi-koneksi ini sangat penting untuk memperoleh pemahaman yang lebih mendalam tentang akar pangkat tiga dan menghargai perannya yang luas dalam matematika.
Pertanyaan Umum Seputar Akar Pangkat Tiga
Bagian ini akan menjawab beberapa pertanyaan umum seputar akar pangkat tiga untuk memberikan pemahaman yang lebih komprehensif.
Pertanyaan 1: Apa saja sifat dasar dari akar pangkat tiga?
Jawaban: Sifat-sifat dasar akar pangkat tiga meliputi:
- Invers dari pangkat tiga
- Distributif terhadap penjumlahan dan pengurangan
- Transitif
- Monotik
Pertanyaan 2: Bagaimana cara menghitung akar pangkat tiga dari suatu bilangan?
Jawaban: Terdapat beberapa metode untuk menghitung akar pangkat tiga, di antaranya:
- Menggunakan kalkulator
- Menggunakan tabel akar
- Menggunakan algoritma perkiraan
Pertanyaan 3: Apa saja aplikasi praktis dari akar pangkat tiga?
Jawaban: Akar pangkat tiga memiliki beragam aplikasi praktis, di antaranya:
- Menghitung volume kubus
- Menghitung jarak tempuh benda yang bergerak dengan percepatan tetap
- Menentukan konsentrasi larutan kimia
Pertanyaan 4: Bagaimana akar pangkat tiga terkait dengan konsep matematika lainnya?
Jawaban: Akar pangkat tiga terhubung dengan berbagai konsep matematika, seperti:
- Limit dan turunan
- Integral
- Persamaan diferensial
- Teori bilangan
Dengan memahami pertanyaan dan jawaban ini, diharapkan dapat meningkatkan pemahaman Anda tentang akar pangkat tiga dan relevansinya dalam matematika dan bidang lainnya.
Selanjutnya, mari kita beralih ke bagian Tips untuk mempelajari strategi praktis dalam menguasai konsep akar pangkat tiga.
Tips Menguasai Akar Pangkat Tiga
Berikut beberapa tips efektif untuk membantu Anda menguasai konsep akar pangkat tiga:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari teknik penyelesaian, luangkan waktu untuk memahami konsep dasar akar pangkat tiga, sifat-sifatnya, dan hubungannya dengan operasi matematika lainnya. Landasan yang kuat akan memudahkan Anda dalam langkah selanjutnya.
Tip 2: Berlatih Menghitung Secara Manual
Meskipun kalkulator tersedia, praktik manual sangat bermanfaat untuk memperkuat pemahaman Anda. Hitung akar pangkat tiga dari berbagai bilangan tanpa bantuan alat bantu. Latihan teratur akan meningkatkan kecepatan dan akurasi Anda.
Tip 3: Gunakan Grafik dan Tabel
Visualisasi dapat sangat membantu dalam memahami akar pangkat tiga. Gunakan grafik dan tabel untuk mengeksplorasi hubungan antara bilangan dan akar pangkat tiganya. Ini akan memberikan wawasan dan intuisi yang berharga.
Tip 4: Terapkan dalam Masalah Kontekstual
Jangan hanya berfokus pada penyelesaian soal latihan. Terapkan konsep akar pangkat tiga dalam masalah kontekstual dari berbagai bidang, seperti fisika, teknik, dan ekonomi. Pemahaman yang mendalam akan berkembang saat Anda menghubungkan konsep dengan dunia nyata.
Dengan mengikuti tips ini secara konsisten, Anda akan meningkatkan pemahaman dan keterampilan Anda dalam bekerja dengan akar pangkat tiga. Konsep ini akan menjadi alat yang ampuh dalam pemecahan masalah dan eksplorasi matematika yang lebih luas.
Kesimpulan
Akar pangkat tiga merupakan konsep matematika penting dengan beragam aplikasi di berbagai bidang. Pemahaman yang mendalam tentang akar pangkat tiga, sifat-sifatnya, dan aplikasinya sangat penting bagi siapa pun yang ingin unggul dalam matematika, fisika, teknik, dan disiplin terkait lainnya.
Artikel ini telah mengeksplorasi berbagai aspek akar pangkat tiga, meliputi definisi, rumus, sifat, aplikasi, sejarah, contoh, koneksi, dan tips untuk menguasainya. Dengan menguasai konsep ini, kita dapat membuka potensi matematika dan memecahkan tantangan dunia nyata dengan lebih efektif.




