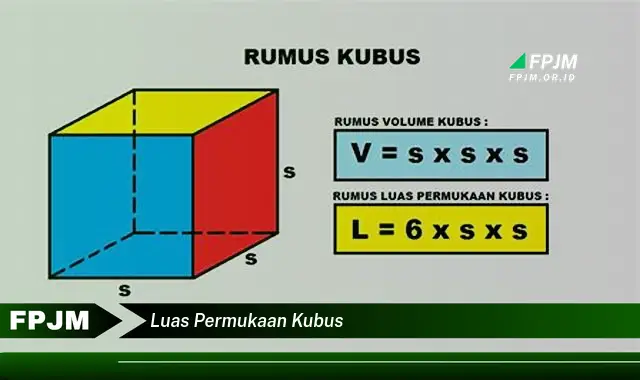
Luas permukaan kubus adalah jumlah luas semua sisi kubus. Karena kubus memiliki 6 sisi yang sama, maka luas permukaan kubus dapat dihitung dengan mengalikan luas salah satu sisinya dengan 6. Dengan kata lain, rumus luas permukaan kubus adalah 6 x (sisi x sisi), dimana “sisi” adalah panjang sisi kubus.
Luas permukaan kubus penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, luas permukaan kubus digunakan untuk menghitung volume kubus. Dalam fisika, luas permukaan kubus digunakan untuk menghitung gaya yang bekerja pada benda yang terendam dalam fluida. Dalam teknik, luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak.
Konsep luas permukaan kubus telah dikenal sejak zaman kuno. Ahli matematika Yunani, Archimedes, adalah salah satu orang pertama yang mempelajari luas permukaan kubus. Archimedes menggunakan konsep luas permukaan kubus untuk menghitung volume bola. Sejak saat itu, konsep luas permukaan kubus terus berkembang dan digunakan dalam berbagai bidang.
luas permukaan kubus
Luas permukaan kubus adalah besaran yang penting dalam matematika, fisika, dan teknik. Berikut adalah 7 aspek penting terkait luas permukaan kubus:
- Definisi
- Rumus
- Satuan
- Aplikasi
- Sejarah
- Contoh
- Keterkaitan
Definisi luas permukaan kubus adalah jumlah luas semua sisi kubus. Rumus luas permukaan kubus adalah 6 x (sisi x sisi), dimana “sisi” adalah panjang sisi kubus. Satuan luas permukaan kubus adalah satuan luas, seperti sentimeter persegi (cm2) atau meter persegi (m2). Luas permukaan kubus memiliki banyak aplikasi dalam berbagai bidang, seperti matematika, fisika, dan teknik. Konsep luas permukaan kubus telah dikenal sejak zaman kuno, dan terus berkembang hingga saat ini.
Definisi
Definisi luas permukaan kubus sangat penting karena menjadi dasar untuk memahami konsep dan perhitungan luas permukaan kubus. Definisi yang jelas dan tepat memungkinkan kita untuk memahami apa yang dimaksud dengan luas permukaan kubus dan bagaimana cara menghitungnya. Hal ini penting dalam berbagai bidang, seperti matematika, fisika, dan teknik, di mana luas permukaan kubus digunakan untuk menyelesaikan berbagai masalah dan perhitungan.
Sebagai contoh, dalam matematika, definisi luas permukaan kubus digunakan untuk menghitung volume kubus. Dalam fisika, definisi luas permukaan kubus digunakan untuk menghitung gaya yang bekerja pada benda yang terendam dalam fluida. Dalam teknik, definisi luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak.
Dengan memahami definisi luas permukaan kubus dengan baik, kita dapat menggunakan konsep ini secara efektif untuk menyelesaikan berbagai masalah dan perhitungan di berbagai bidang. Definisi yang jelas dan tepat menjadi landasan bagi pemahaman dan aplikasi yang benar dari konsep luas permukaan kubus.
Rumus
Rumus luas permukaan kubus sangat penting karena memungkinkan kita untuk menghitung luas permukaan kubus dengan mudah dan akurat. Rumus ini diturunkan dari konsep dasar geometri dan memberikan hubungan yang jelas antara panjang sisi kubus dan luas permukaannya.
-
Menggunakan panjang sisi
Rumus luas permukaan kubus yang paling umum digunakan adalah 6 x (sisi x sisi), di mana “sisi” adalah panjang sisi kubus. Rumus ini mudah digunakan dan dapat diterapkan pada semua jenis kubus. -
Menggunakan diagonal sisi
Rumus alternatif untuk luas permukaan kubus adalah 2 x (diagonal sisi x diagonal sisi), di mana “diagonal sisi” adalah diagonal salah satu sisi kubus. Rumus ini berguna ketika panjang diagonal sisi diketahui, tetapi panjang sisi tidak diketahui. -
Menggunakan volume
Rumus luas permukaan kubus juga dapat diturunkan dari volume kubus. Rumus ini menyatakan bahwa luas permukaan kubus adalah 6 x (volume / sisi), di mana “volume” adalah volume kubus dan “sisi” adalah panjang sisi kubus. Rumus ini berguna ketika volume kubus diketahui, tetapi panjang sisi tidak diketahui. -
Aplikasi dalam kehidupan nyata
Rumus luas permukaan kubus memiliki banyak aplikasi dalam kehidupan nyata, seperti:- Menghitung luas permukaan kotak atau balok
- Menghitung luas permukaan benda berbentuk kubus, seperti dadu atau balok es
- Menghitung luas permukaan benda yang dilapisi dengan bahan berbentuk kubus, seperti keramik atau batu bata
Dengan memahami rumus luas permukaan kubus dan aplikasinya, kita dapat menyelesaikan berbagai masalah dan perhitungan yang melibatkan kubus dan benda berbentuk kubus lainnya.
Satuan Luas Permukaan Kubus
Satuan luas permukaan kubus sangat penting karena memungkinkan kita untuk menyatakan dan membandingkan luas permukaan kubus dengan jelas dan tepat. Pemilihan satuan yang sesuai tergantung pada konteks dan tujuan pengukuran.
-
Satuan Umum
Satuan umum untuk luas permukaan kubus adalah satuan luas, seperti sentimeter persegi (cm2) atau meter persegi (m2). Satuan-satuan ini mudah dipahami dan digunakan dalam berbagai aplikasi. -
Satuan Khusus
Dalam konteks tertentu, satuan khusus dapat digunakan untuk luas permukaan kubus. Misalnya, dalam fisika, satuan barn (b) digunakan untuk menyatakan luas penampang hamburan partikel nuklir. 1 barn sama dengan 10-28 m2. -
Konversi Satuan
Jika diperlukan, luas permukaan kubus dapat dikonversi dari satu satuan ke satuan lainnya menggunakan faktor konversi yang sesuai. Misalnya, untuk mengonversi dari cm2 ke m2, kita kalikan dengan faktor 10-4. -
Implikasi dalam Perhitungan
Pemilihan satuan yang tepat untuk luas permukaan kubus berimplikasi pada perhitungan selanjutnya. Misalnya, dalam menghitung volume kubus, jika luas permukaan kubus dinyatakan dalam cm2, maka volume akan dinyatakan dalam cm3.
Dengan memahami satuan luas permukaan kubus dan implikasinya, kita dapat memastikan akurasi dan konsistensi dalam pengukuran dan perhitungan yang melibatkan kubus.
Aplikasi
Luas permukaan kubus memiliki banyak aplikasi dalam berbagai bidang, antara lain:
-
Matematika
Dalam matematika, luas permukaan kubus digunakan untuk menghitung volume kubus, mencari luas permukaan bangun ruang yang tersusun dari kubus, dan menyelesaikan berbagai masalah geometri. -
Fisika
Dalam fisika, luas permukaan kubus digunakan untuk menghitung gaya yang bekerja pada benda yang terendam dalam fluida, menghitung hambatan listrik, dan menganalisis perpindahan panas. -
Teknik
Dalam teknik, luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak, dan merancang struktur dan mesin yang melibatkan bentuk kubus. -
Kehidupan Sehari-hari
Dalam kehidupan sehari-hari, luas permukaan kubus digunakan untuk menghitung luas permukaan benda-benda yang berbentuk kubus, seperti dadu, balok es, dan kemasan kubus.
Aplikasi luas permukaan kubus sangat luas dan mencakup berbagai bidang ilmu pengetahuan dan kehidupan praktis. Dengan memahami konsep dan rumus luas permukaan kubus, kita dapat menyelesaikan berbagai masalah dan perhitungan yang melibatkan benda berbentuk kubus.
Sejarah
Konsep luas permukaan kubus telah dikenal sejak zaman kuno. Ahli matematika Yunani, Archimedes, adalah salah satu orang pertama yang mempelajari luas permukaan kubus. Archimedes menggunakan konsep luas permukaan kubus untuk menghitung volume bola. Sejak saat itu, konsep luas permukaan kubus terus berkembang dan digunakan dalam berbagai bidang.
-
Matematika
Dalam matematika, konsep luas permukaan kubus digunakan untuk menghitung volume kubus dan menyelesaikan berbagai masalah geometri. Misalnya, Archimedes menggunakan konsep luas permukaan kubus untuk membuktikan bahwa volume bola adalah 2/3 dari volume silinder yang membungkusnya. -
Fisika
Dalam fisika, konsep luas permukaan kubus digunakan untuk menghitung gaya yang bekerja pada benda yang terendam dalam fluida. Misalnya, gaya apung pada benda yang terendam dalam fluida sebanding dengan luas permukaan benda tersebut. -
Teknik
Dalam teknik, konsep luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak. Misalnya, luas permukaan balok digunakan untuk menghitung luas permukaan total sebuah bangunan. -
Kehidupan Sehari-hari
Dalam kehidupan sehari-hari, konsep luas permukaan kubus digunakan untuk menghitung luas permukaan benda-benda yang berbentuk kubus, seperti dadu atau kemasan kubus. Misalnya, kita dapat menggunakan konsep luas permukaan kubus untuk menghitung luas permukaan sebuah kubus es.
Dengan memahami sejarah dan perkembangan konsep luas permukaan kubus, kita dapat lebih menghargai pentingnya konsep ini dalam berbagai bidang ilmu pengetahuan dan kehidupan praktis.
Contoh
Contoh sangat penting dalam memahami konsep luas permukaan kubus karena memberikan representasi konkret dan praktis dari konsep abstrak. Contoh membantu memvisualisasikan konsep, menghubungkannya dengan pengalaman nyata, dan memperjelas penerapannya dalam berbagai situasi.
-
Kubus dalam Kehidupan Sehari-hari
Salah satu contoh yang paling umum dari luas permukaan kubus adalah dadu. Setiap sisi dadu adalah persegi, dan luas permukaan dadu sama dengan jumlah luas keenam sisinya. Contoh lain dari luas permukaan kubus adalah kemasan kubus, seperti kotak sepatu atau kardus. Luas permukaan kemasan kubus digunakan untuk menghitung luas permukaan total kemasan dan menentukan jumlah bahan yang dibutuhkan untuk membuatnya.
-
Kubus dalam Matematika
Dalam matematika, kubus digunakan untuk menghitung volume dan luas permukaan bangun ruang yang lebih kompleks. Misalnya, luas permukaan kubus dapat digunakan untuk menghitung luas permukaan prisma atau limas yang memiliki alas berbentuk kubus. Contoh lain adalah penggunaan luas permukaan kubus untuk menghitung volume bola, seperti yang dilakukan oleh Archimedes.
-
Kubus dalam Fisika
Dalam fisika, luas permukaan kubus penting untuk menghitung gaya yang bekerja pada benda yang terendam dalam fluida. Misalnya, gaya apung pada benda yang terendam dalam air sebanding dengan luas permukaan benda tersebut. Luas permukaan kubus juga digunakan dalam perhitungan perpindahan panas dan hambatan listrik.
-
Kubus dalam Teknik
Dalam teknik, luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak. Misalnya, luas permukaan balok digunakan untuk menghitung luas permukaan total sebuah bangunan atau jembatan. Luas permukaan kubus juga penting dalam desain dan analisis struktur dan mesin yang melibatkan bentuk kubus.
Contoh-contoh ini menunjukkan bahwa luas permukaan kubus memiliki aplikasi yang luas dalam berbagai bidang, mulai dari kehidupan sehari-hari hingga matematika, fisika, dan teknik. Dengan memahami contoh-contoh ini, kita dapat memperoleh pemahaman yang lebih mendalam tentang konsep luas permukaan kubus dan penerapannya dalam dunia nyata.
Keterkaitan
Luas permukaan kubus memiliki keterkaitan yang erat dengan berbagai konsep dan bidang lainnya. Keterkaitan ini memperluas pemahaman kita tentang luas permukaan kubus dan memungkinkan kita untuk menerapkannya dalam konteks yang lebih luas.
-
Geometri
Dalam geometri, luas permukaan kubus terkait erat dengan konsep volume dan luas permukaan bangun ruang lainnya. Misalnya, luas permukaan kubus dapat digunakan untuk menghitung volume kubus dan luas permukaan prisma atau limas yang memiliki alas berbentuk kubus.
-
Fisika
Dalam fisika, luas permukaan kubus berkaitan dengan konsep gaya dan perpindahan panas. Luas permukaan kubus digunakan untuk menghitung gaya apung pada benda yang terendam dalam fluida dan menghitung laju perpindahan panas melalui benda.
-
Teknik
Dalam teknik, luas permukaan kubus berkaitan dengan konsep desain dan konstruksi. Luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak, dan menentukan jumlah bahan yang dibutuhkan untuk membuatnya.
-
Kehidupan Sehari-hari
Dalam kehidupan sehari-hari, luas permukaan kubus berkaitan dengan konsep kemasan dan penyimpanan. Luas permukaan kubus digunakan untuk menghitung luas permukaan kemasan kubus, seperti kotak sepatu atau kardus, dan menentukan volume benda yang dapat disimpan di dalamnya.
Keterkaitan luas permukaan kubus dengan berbagai konsep dan bidang lainnya menunjukkan bahwa konsep ini memiliki aplikasi yang luas dan penting dalam berbagai aspek kehidupan. Dengan memahami keterkaitan ini, kita dapat memanfaatkan luas permukaan kubus untuk menyelesaikan masalah dan membuat keputusan dalam berbagai konteks.
Pertanyaan Umum tentang Luas Permukaan Kubus
Berikut adalah beberapa pertanyaan umum tentang luas permukaan kubus:
Pertanyaan 1: Bagaimana cara menghitung luas permukaan kubus?
Luas permukaan kubus dapat dihitung dengan mengalikan panjang sisi kubus dengan 6. Rumus luas permukaan kubus adalah 6 x (sisi x sisi), di mana “sisi” adalah panjang sisi kubus.
Pertanyaan 2: Apa saja aplikasi luas permukaan kubus?
Luas permukaan kubus memiliki banyak aplikasi dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, luas permukaan kubus digunakan untuk menghitung volume kubus dan luas permukaan bangun ruang yang tersusun dari kubus. Dalam fisika, luas permukaan kubus digunakan untuk menghitung gaya yang bekerja pada benda yang terendam dalam fluida. Dalam teknik, luas permukaan kubus digunakan untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak.
Pertanyaan 3: Mengapa luas permukaan kubus penting?
Luas permukaan kubus penting karena memungkinkan kita untuk menghitung luas permukaan benda yang berbentuk kubus, seperti balok atau kotak. Luas permukaan kubus juga penting dalam berbagai perhitungan, seperti menghitung volume kubus dan gaya yang bekerja pada benda yang terendam dalam fluida.
Pertanyaan 4: Bagaimana cara menggunakan luas permukaan kubus dalam kehidupan sehari-hari?
Luas permukaan kubus dapat digunakan dalam kehidupan sehari-hari untuk menghitung luas permukaan benda-benda yang berbentuk kubus, seperti dadu atau kemasan kubus. Misalnya, kita dapat menggunakan luas permukaan kubus untuk menghitung luas permukaan sebuah kubus es atau luas permukaan sebuah kotak sepatu.
Dengan memahami konsep dan aplikasi luas permukaan kubus, kita dapat menyelesaikan berbagai masalah dan perhitungan yang melibatkan benda berbentuk kubus.
Untuk informasi lebih lanjut tentang luas permukaan kubus, silakan lihat artikel Tips di bawah ini.
Tips Menguasai Konsep Luas Permukaan Kubus
Untuk menguasai konsep luas permukaan kubus, berikut beberapa tips yang dapat membantu:
Tip 1: Pahami Konsep Dasar Geometri
Sebelum mempelajari luas permukaan kubus, pastikan untuk memahami konsep dasar geometri, seperti persegi, balok, dan volume. Konsep-konsep ini akan menjadi dasar untuk memahami luas permukaan kubus.
Tip 2: Hafalkan Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus adalah 6 x (sisi x sisi), di mana “sisi” adalah panjang sisi kubus. Hafalkan rumus ini dan pahami bagaimana rumus tersebut diturunkan.
Tip 3: Latihan Soal Secara Teratur
Latihan soal secara teratur akan membantu Anda memahami konsep luas permukaan kubus dan menerapkannya dalam berbagai situasi. Carilah soal-soal latihan dari berbagai sumber, seperti buku teks, lembar kerja, atau situs web pendidikan.
Tip 4: Terapkan dalam Kehidupan Nyata
Cobalah untuk menerapkan konsep luas permukaan kubus dalam kehidupan nyata. Misalnya, hitung luas permukaan kubus es atau luas permukaan kemasan kubus. Hal ini akan membantu Anda memahami relevansi dan aplikasi praktis dari konsep ini.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang luas permukaan kubus dan menerapkannya dengan percaya diri dalam berbagai situasi.
Kesimpulannya, luas permukaan kubus adalah konsep penting dalam matematika dan memiliki berbagai aplikasi dalam bidang lain. Dengan memahami konsep ini secara mendalam, Anda dapat menyelesaikan masalah dan membuat keputusan yang lebih tepat.
Kesimpulan
Luas permukaan kubus merupakan konsep penting dalam matematika dan memiliki berbagai aplikasi dalam bidang lain, seperti fisika dan teknik. Konsep ini digunakan untuk menghitung luas permukaan benda berbentuk kubus, seperti balok atau kotak, serta untuk menghitung volume kubus dan gaya yang bekerja pada benda yang terendam dalam fluida.
Dengan memahami konsep luas permukaan kubus secara mendalam, kita dapat menyelesaikan masalah dan membuat keputusan yang lebih tepat dalam berbagai situasi. Misalnya, kita dapat menggunakan konsep ini untuk menghitung luas permukaan sebuah gedung atau untuk menghitung gaya apung pada sebuah kapal.




