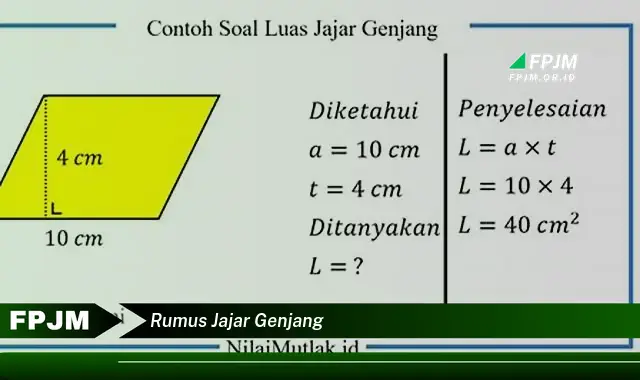
Rumus jajar genjang adalah rumus yang digunakan untuk mencari luas dan keliling jajar genjang. Luas jajar genjang dapat dicari dengan mengalikan panjang alas dengan tinggi jajar genjang. Sedangkan keliling jajar genjang dapat dicari dengan menjumlahkan panjang keempat sisinya.
Rumus jajar genjang sangat penting dalam matematika karena digunakan untuk menyelesaikan berbagai soal yang berkaitan dengan jajar genjang. Selain itu, rumus jajar genjang juga sering digunakan dalam bidang arsitektur dan teknik untuk menghitung luas dan keliling bangunan atau benda-benda yang berbentuk jajar genjang.
Sejarah rumus jajar genjang pertama kali ditemukan oleh matematikawan Yunani, Pythagoras, pada abad ke-6 SM. Pythagoras menemukan rumus ini ketika sedang mempelajari sifat-sifat geometri. Rumus jajar genjang kemudian dikembangkan oleh matematikawan lainnya, seperti Euclid dan Archimedes, dan menjadi salah satu rumus dasar dalam matematika.
Rumus Jajar Genjang
Rumus jajar genjang merupakan bagian penting dalam matematika, terutama untuk menghitung luas dan keliling jajar genjang. Rumus ini memiliki beberapa aspek penting, antara lain:
- Luas
- Keliling
- Alas
- Tinggi
- Diagonal
- Sudut
- Bangun datar
Luas jajar genjang dihitung dengan mengalikan panjang alas dengan tinggi. Keliling jajar genjang dihitung dengan menjumlahkan panjang keempat sisinya. Diagonal jajar genjang membagi jajar genjang menjadi dua segitiga sama luas. Sudut-sudut jajar genjang berhadapan sama besar, dan sudut-sudut yang berdekatan jumlahnya 180 derajat. Jajar genjang merupakan salah satu jenis bangun datar yang memiliki empat sisi dan empat sudut.
Luas
Luas merupakan besaran yang menyatakan ukuran daerah suatu permukaan. Dalam konteks rumus jajar genjang, luas digunakan untuk menghitung ukuran permukaan jajar genjang tersebut.
-
Menghitung Luas Jajar Genjang
Rumus luas jajar genjang digunakan untuk menghitung ukuran luas permukaan jajar genjang. Rumus ini melibatkan perkalian antara panjang alas dan tinggi jajar genjang.
-
Satuan Luas
Hasil perhitungan luas jajar genjang dinyatakan dalam satuan luas, seperti meter persegi (m), sentimeter persegi (cm), atau kilometer persegi (km). Pemilihan satuan luas disesuaikan dengan konteks dan kebutuhan.
-
Aplikasi dalam Kehidupan Nyata
Rumus luas jajar genjang banyak digunakan dalam kehidupan nyata, seperti menghitung luas lantai, luas dinding, atau luas tanah. Dengan mengetahui luas suatu permukaan, kita dapat merencanakan dan menggunakannya secara efektif.
-
Hubungan dengan Rumus Jajar Genjang Lainnya
Rumus luas jajar genjang terkait dengan rumus jajar genjang lainnya, seperti rumus keliling dan rumus diagonal. Ketiga rumus ini saling melengkapi dan dapat digunakan untuk menyelesaikan berbagai permasalahan yang melibatkan jajar genjang.
Dengan memahami konsep luas dan cara menghitungnya menggunakan rumus jajar genjang, kita dapat menyelesaikan permasalahan yang berkaitan dengan pengukuran permukaan jajar genjang secara akurat dan efisien.
Keliling
Keliling merupakan besaran yang menyatakan panjang sekeliling suatu bangun datar. Dalam konteks rumus jajar genjang, keliling digunakan untuk menghitung panjang sekeliling jajar genjang tersebut.
Menghitung Keliling Jajar Genjang
Rumus keliling jajar genjang digunakan untuk menghitung panjang sekeliling jajar genjang. Rumus ini melibatkan penjumlahan panjang keempat sisi jajar genjang.
Satuan Keliling
Hasil perhitungan keliling jajar genjang dinyatakan dalam satuan panjang, seperti meter (m), sentimeter (cm), atau kilometer (km). Pemilihan satuan panjang disesuaikan dengan konteks dan kebutuhan.
Aplikasi dalam Kehidupan Nyata
Rumus keliling jajar genjang banyak digunakan dalam kehidupan nyata, seperti menghitung keliling lapangan, keliling pagar, atau keliling kolam renang. Dengan mengetahui keliling suatu bangun datar, kita dapat merencanakan dan menggunakannya secara efektif.
Hubungan dengan Rumus Jajar Genjang Lainnya
Rumus keliling jajar genjang terkait dengan rumus jajar genjang lainnya, seperti rumus luas dan rumus diagonal. Ketiga rumus ini saling melengkapi dan dapat digunakan untuk menyelesaikan berbagai permasalahan yang melibatkan jajar genjang.
Dengan memahami konsep keliling dan cara menghitungnya menggunakan rumus jajar genjang, kita dapat menyelesaikan permasalahan yang berkaitan dengan pengukuran keliling jajar genjang secara akurat dan efisien.
Alas
Dalam rumus jajar genjang, alas merupakan salah satu unsur penting yang menentukan luas dan keliling jajar genjang. Alas adalah sisi mendatar dari jajar genjang yang sejajar dengan sisi atasnya. Panjang alas berdampak langsung pada nilai luas dan keliling jajar genjang.
Jika alas jajar genjang lebih panjang, maka luas jajar genjang akan semakin besar. Begitu pula sebaliknya, jika alas jajar genjang lebih pendek, maka luas jajar genjang akan semakin kecil. Alas juga berpengaruh pada keliling jajar genjang. Semakin panjang alas jajar genjang, maka keliling jajar genjang akan semakin besar. Hal ini karena alas merupakan salah satu dari empat sisi jajar genjang yang dijumlahkan untuk menghitung keliling.
Dalam kehidupan nyata, memahami hubungan antara alas dan rumus jajar genjang sangat penting. Misalnya, dalam bidang arsitektur dan konstruksi, menghitung luas dan keliling lantai atau dinding yang berbentuk jajar genjang memerlukan pengukuran alas yang tepat. Selain itu, dalam bidang pertanian, menghitung luas lahan berbentuk jajar genjang juga memerlukan pengukuran alas yang akurat untuk menentukan kebutuhan pupuk dan bahan tanam.
Tinggi
Tinggi merupakan unsur penting lainnya dalam rumus jajar genjang yang menentukan luas dan keliling jajar genjang. Tinggi adalah sisi tegak lurus dari jajar genjang yang diukur dari alas ke sisi atas. Panjang tinggi berdampak langsung pada nilai luas dan keliling jajar genjang.
-
Menentukan Luas Jajar Genjang
Dalam rumus jajar genjang, tinggi berperan penting dalam menentukan luas jajar genjang. Semakin panjang tinggi jajar genjang, maka luas jajar genjang akan semakin besar. Begitu pula sebaliknya, jika tinggi jajar genjang lebih pendek, maka luas jajar genjang akan semakin kecil.
-
Menentukan Keliling Jajar Genjang
Tinggi tidak secara langsung mempengaruhi keliling jajar genjang. Namun, tinggi berperan dalam menentukan panjang sisi miring jajar genjang, yang pada akhirnya mempengaruhi keliling jajar genjang.
-
Aplikasi dalam Kehidupan Nyata
Memahami hubungan antara tinggi dan rumus jajar genjang sangat penting dalam berbagai bidang. Misalnya, dalam bidang arsitektur dan konstruksi, menghitung luas dan keliling dinding atau atap yang berbentuk jajar genjang memerlukan pengukuran tinggi yang tepat. Selain itu, dalam bidang pertanian, menghitung luas lahan berbentuk jajar genjang juga memerlukan pengukuran tinggi yang akurat untuk menentukan kebutuhan pupuk dan bahan tanam.
Dengan memahami konsep tinggi dan hubungannya dengan rumus jajar genjang, kita dapat menyelesaikan permasalahan yang berkaitan dengan pengukuran luas dan keliling jajar genjang secara akurat dan efisien.
Diagonal
Dalam rumus jajar genjang, diagonal memiliki peran penting dalam menentukan berbagai aspek jajar genjang, seperti luas, keliling, dan sifat-sifat lainnya.
-
Membagi Jajar Genjang Menjadi Dua Segitiga Sama Luas
Diagonal jajar genjang membagi jajar genjang menjadi dua segitiga yang sama luas. Sifat ini dapat dimanfaatkan untuk menyelesaikan berbagai permasalahan yang berkaitan dengan jajar genjang, seperti mencari luas atau keliling.
-
Menentukan Panjang Sisi Miring
Diagonal jajar genjang dapat digunakan untuk menentukan panjang sisi miring jajar genjang. Dalam rumus jajar genjang, panjang sisi miring dapat dihitung menggunakan teorema Pythagoras, di mana diagonal jajar genjang merupakan sisi miringnya.
-
Mencirikan Jajar Genjang
Diagonal jajar genjang dapat digunakan untuk mencirikan jenis jajar genjang. Jika diagonal jajar genjang saling tegak lurus, maka jajar genjang tersebut adalah persegi panjang. Jika diagonal jajar genjang sama panjang, maka jajar genjang tersebut adalah belah ketupat.
-
Menentukan Panjang Diagonal
Rumus jajar genjang juga dapat digunakan untuk menentukan panjang diagonal jajar genjang. Panjang diagonal dapat dihitung menggunakan rumus yang melibatkan panjang alas, tinggi, dan sisi miring jajar genjang.
Dengan memahami hubungan antara diagonal dan rumus jajar genjang, kita dapat menyelesaikan berbagai permasalahan yang berkaitan dengan jajar genjang secara akurat dan efisien. Diagonal berperan penting dalam menentukan karakteristik dan sifat-sifat jajar genjang, menjadikannya unsur penting dalam rumus jajar genjang.
Sudut
Dalam rumus jajar genjang, sudut memiliki peran penting dalam menentukan sifat-sifat dan karakteristik jajar genjang. Sudut pada jajar genjang saling berkaitan dan memengaruhi perhitungan luas dan keliling jajar genjang.
-
Jenis-jenis Sudut
Jajar genjang memiliki empat sudut yang terbagi menjadi dua jenis, yaitu sudut siku-siku dan sudut lancip. Sudut siku-siku adalah sudut yang besarnya 90 derajat, sedangkan sudut lancip adalah sudut yang besarnya kurang dari 90 derajat. Sifat sudut-sudut ini memengaruhi bentuk dan sifat jajar genjang secara keseluruhan.
-
Jumlah Sudut Berhadapan
Salah satu sifat penting sudut pada jajar genjang adalah jumlah sudut-sudut yang berhadapan selalu sama dengan 180 derajat. Sifat ini berlaku untuk semua jajar genjang,.
-
Hubungan dengan Sifat Lain
Sudut-sudut pada jajar genjang juga terkait dengan sifat-sifat lainnya, seperti kesamaan panjang sisi dan diagonal. Dalam jajar genjang, sisi-sisi yang berhadapan sama panjang, dan diagonal-diagonalnya saling membagi dua sama panjang.
-
Aplikasi dalam Kehidupan Nyata
Pemahaman tentang sudut pada jajar genjang diterapkan dalam berbagai bidang, seperti arsitektur dan teknik. Dalam arsitektur, sudut jajar genjang digunakan untuk menentukan bentuk dan desain bangunan. Sementara dalam teknik, sudut jajar genjang digunakan untuk menghitung kekuatan dan stabilitas struktur.
Dengan memahami hubungan antara sudut dan rumus jajar genjang, kita dapat menyelesaikan berbagai permasalahan yang berkaitan dengan jajar genjang secara akurat dan efisien. Sudut memainkan peran penting dalam menentukan sifat-sifat geometris jajar genjang, menjadikannya unsur penting dalam rumus jajar genjang.
Bangun Datar
Bangun datar merupakan salah satu konsep dasar dalam geometri yang membahas tentang bentuk-bentuk dua dimensi. Berbagai bangun datar memiliki sifat dan karakteristik yang berbeda-beda, salah satunya adalah jajar genjang. Rumus jajar genjang merupakan bagian penting dalam geometri yang digunakan untuk menghitung luas dan keliling jajar genjang.
Sebagai sebuah bangun datar, jajar genjang memiliki ciri-ciri khusus, seperti memiliki empat sisi, empat sudut, dan dua pasang sisi yang sejajar. Rumus jajar genjang diturunkan berdasarkan sifat-sifat tersebut, sehingga memiliki keterkaitan yang erat dengan konsep bangun datar. Memahami hubungan antara bangun datar dan rumus jajar genjang sangat penting, karena memungkinkan kita untuk menyelesaikan berbagai permasalahan yang melibatkan jajar genjang.
Dalam kehidupan nyata, rumus jajar genjang banyak diaplikasikan dalam berbagai bidang, seperti arsitektur, teknik sipil, dan pertanian. Contohnya, dalam arsitektur, rumus jajar genjang digunakan untuk menghitung luas lantai atau dinding yang berbentuk jajar genjang. Sementara dalam teknik sipil, rumus jajar genjang digunakan untuk menghitung luas permukaan jembatan atau bangunan lainnya yang memiliki bentuk jajar genjang. Dengan memahami keterkaitan antara bangun datar dan rumus jajar genjang, kita dapat memperoleh pemahaman yang lebih komprehensif tentang geometri dan penerapannya dalam kehidupan sehari-hari.
Tanya Jawab Seputar Rumus Jajar Genjang
Bagian ini akan menjawab beberapa pertanyaan umum yang sering diajukan terkait rumus jajar genjang. Dengan memahami konsep dan aplikasi rumus jajar genjang, kita dapat menyelesaikan permasalahan yang melibatkan bangun datar ini secara efektif.
Pertanyaan 1:
Bagaimana cara menghitung luas jajar genjang?
Jawaban:
Luas jajar genjang dapat dihitung dengan mengalikan panjang alas dengan tinggi jajar genjang.
Pertanyaan 2:
Apa saja faktor yang memengaruhi keliling jajar genjang?
Jawaban:
Keliling jajar genjang dipengaruhi oleh panjang keempat sisinya.
Pertanyaan 3:
Bagaimana rumus jajar genjang dapat diterapkan dalam kehidupan nyata?
Jawaban:
Rumus jajar genjang banyak digunakan dalam bidang arsitektur, teknik sipil, dan pertanian untuk menghitung luas dan keliling benda atau permukaan yang berbentuk jajar genjang.
Pertanyaan 4:
Apa saja sifat-sifat khusus jajar genjang yang berkaitan dengan rumus jajar genjang?
Jawaban:
Salah satu sifat khusus jajar genjang adalah memiliki dua pasang sisi yang sejajar dan empat sudut yang berhadapan sama besar.
Dengan memahami pertanyaan dan jawaban yang telah dibahas, kita dapat memperoleh pemahaman yang lebih mendalam tentang rumus jajar genjang dan penerapannya dalam berbagai bidang.
Selanjutnya, kita akan membahas beberapa tips dalam menggunakan rumus jajar genjang untuk menyelesaikan permasalahan matematika.
Tips Menggunakan Rumus Jajar Genjang
Berikut adalah beberapa tips untuk menggunakan rumus jajar genjang secara efektif dalam menyelesaikan permasalahan matematika:
Tip 1:
Pahami konsep dasar jajar genjang, seperti sifat-sifatnya, jenis-jenisnya, dan hubungan antarunsurnya.
Tip 2:
Identifikasi dengan jelas besaran yang akan dicari, apakah luas atau keliling jajar genjang.
Tip 3:
Pastikan satuan yang digunakan untuk panjang alas dan tinggi jajar genjang konsisten, sehingga hasil perhitungan juga memiliki satuan yang sesuai.
Tip 4:
Perhatikan dengan seksama apakah jajar genjang yang diberikan memiliki sifat khusus, seperti persegi panjang atau belah ketupat, yang dapat menyederhanakan perhitungan.
Dengan mengikuti tips-tips ini, kita dapat meningkatkan akurasi dan efisiensi dalam menggunakan rumus jajar genjang untuk menyelesaikan permasalahan matematika.
Dengan memahami konsep dasar, sifat-sifat, dan tips menggunakan rumus jajar genjang, kita dapat menguasai teknik perhitungan luas dan keliling jajar genjang secara efektif. Rumus ini menjadi alat yang penting dalam berbagai bidang, sehingga pemahaman yang baik tentang rumus jajar genjang sangat bermanfaat.
Kesimpulan Rumus Jajar Genjang
Rumus jajar genjang merupakan konsep penting dalam matematika yang digunakan untuk menghitung luas dan keliling jajar genjang. Rumus ini memiliki keterkaitan yang erat dengan sifat-sifat jajar genjang, seperti memiliki dua pasang sisi sejajar dan empat sudut yang berhadapan sama besar. Memahami rumus jajar genjang menjadi sangat penting karena banyak diaplikasikan dalam berbagai bidang kehidupan, seperti arsitektur, teknik sipil, dan pertanian.
Dengan memahami konsep dasar, sifat-sifat, dan tips penggunaan rumus jajar genjang, kita dapat menyelesaikan permasalahan matematika yang melibatkan bangun datar ini secara efektif dan akurat. Rumus jajar genjang akan terus menjadi alat yang bermanfaat dalam berbagai bidang, sehingga menguasai teknik perhitungannya sangat penting.




