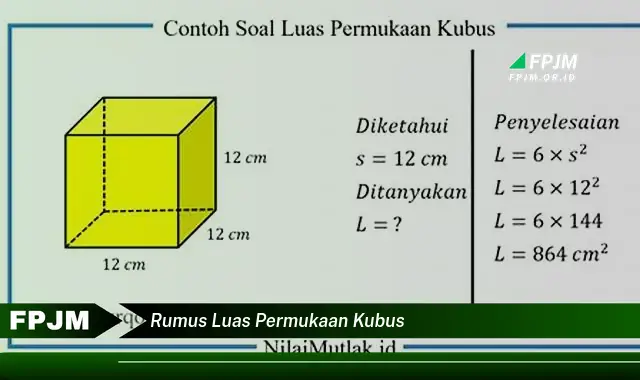
Rumus luas permukaan kubus adalah rumus yang digunakan untuk menghitung luas permukaan bangun ruang kubus. Rumus ini menyatakan bahwa luas permukaan kubus sama dengan enam kali luas salah satu sisinya. Misalnya, jika panjang sisi kubus adalah 5 cm, maka luas permukaan kubusnya adalah 6 x 5 cm x 5 cm = 150 cm2.
Rumus luas permukaan kubus sangat penting dalam bidang matematika dan teknik. Rumus ini digunakan untuk menghitung kebutuhan bahan bangunan, seperti cat atau ubin, yang diperlukan untuk menutupi permukaan kubus. Selain itu, rumus ini juga digunakan dalam perhitungan volume dan luas permukaan bangun ruang lainnya yang berhubungan dengan kubus, seperti balok dan prisma.
Rumus luas permukaan kubus pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM. Rumus ini kemudian dikembangkan lebih lanjut oleh matematikawan India dan Arab pada abad pertengahan. Seiring perkembangan ilmu pengetahuan dan teknologi, rumus ini terus digunakan dan disempurnakan hingga saat ini.
Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus sangat penting dalam bidang matematika dan teknik. Rumus ini memiliki beberapa aspek penting, yaitu:
- Kubus: Bangun ruang yang memiliki enam sisi berbentuk persegi
- Luas permukaan: Jumlah luas semua sisi permukaan
- Sisi: Garis yang menghubungkan dua titik sudut pada sebuah sisi
- Persegi: Bangun datar yang memiliki empat sisi sama panjang
- Panjang sisi: Jarak antara dua titik sudut pada sebuah sisi
- Enam: Jumlah sisi sebuah kubus
- Kali: Operasi matematika untuk mengalikan dua bilangan
Aspek-aspek tersebut saling terkait dan membentuk rumus luas permukaan kubus, yaitu L = 6 x s2, di mana L adalah luas permukaan kubus dan s adalah panjang sisi kubus. Rumus ini digunakan untuk menghitung luas permukaan kubus dengan mudah dan cepat.
Kubus
Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi. Setiap sisi kubus memiliki luas yang sama, dan semua sudutnya siku-siku. Kubus merupakan salah satu bangun ruang yang paling umum dijumpai dalam kehidupan sehari-hari, seperti pada dadu, kotak sabun, dan kemasan makanan.
Rumus luas permukaan kubus sangat terkait dengan sifat-sifat kubus tersebut. Karena kubus memiliki enam sisi berbentuk persegi, maka luas permukaan kubus dapat dihitung dengan menjumlahkan luas keenam sisinya. Setiap sisi kubus memiliki luas yang sama, yaitu s2, di mana s adalah panjang sisi kubus. Oleh karena itu, rumus luas permukaan kubus menjadi L = 6 x s2.
Rumus luas permukaan kubus sangat penting dalam berbagai bidang, seperti matematika, teknik, dan desain. Rumus ini digunakan untuk menghitung kebutuhan bahan bangunan, seperti cat atau ubin, yang diperlukan untuk menutupi permukaan kubus. Selain itu, rumus ini juga digunakan dalam perhitungan volume dan luas permukaan bangun ruang lainnya yang berhubungan dengan kubus, seperti balok dan prisma.
Luas Permukaan
Luas permukaan suatu bangun ruang merupakan besaran yang menyatakan jumlah luas semua sisi permukaan bangun ruang tersebut. Dalam konteks rumus luas permukaan kubus, luas permukaan merupakan besaran yang dihitung untuk menentukan seberapa besar area yang menutupi seluruh sisi kubus.
-
Peranan Luas Permukaan dalam Kubus
Pada kubus, luas permukaan berperan penting dalam menentukan kebutuhan material untuk menutupi atau mengecat seluruh permukaan kubus. Misalnya, jika kita ingin mengecat sebuah kubus dengan sisi 10 cm, maka kita perlu mengetahui luas permukaan kubus tersebut untuk menentukan jumlah cat yang dibutuhkan.
-
Komponen Luas Permukaan Kubus
Luas permukaan kubus terdiri dari enam sisi persegi yang identik. Setiap sisi persegi memiliki luas yang sama, yaitu sisi dikali sisi (s x s). Dengan demikian, luas permukaan kubus merupakan penjumlahan dari luas keenam sisinya, atau 6 x s2.
-
Implikasi Luas Permukaan Kubus
Mengetahui luas permukaan kubus sangat penting dalam berbagai aplikasi praktis. Selain untuk menentukan kebutuhan material, luas permukaan kubus juga digunakan dalam perhitungan volume kubus, perhitungan luas permukaan bangun ruang lainnya yang berhubungan dengan kubus, serta dalam bidang teknik dan desain.
Dengan demikian, luas permukaan dalam rumus luas permukaan kubus merupakan besaran yang sangat penting untuk memahami sifat-sifat kubus dan untuk menyelesaikan berbagai masalah yang berkaitan dengan kubus.
Sisi
Dalam konteks rumus luas permukaan kubus, sisi merupakan faktor penentu yang sangat penting. Sisi kubus adalah garis lurus yang menghubungkan dua titik sudut pada sebuah bidang permukaan kubus. Panjang sisi kubus menentukan besarnya luas permukaan kubus.
-
Komponen Sisi Kubus
Setiap kubus memiliki enam sisi yang identik. Keenam sisi tersebut tersusun dari garis-garis sisi yang saling tegak lurus dan membentuk sudut siku-siku.
-
Pengaruh Sisi terhadap Luas Permukaan
Luas permukaan kubus berbanding lurus dengan kuadrat panjang sisinya. Dengan kata lain, jika panjang sisi kubus diperbesar dua kali, maka luas permukaan kubus akan menjadi empat kali lebih besar.
-
Implikasi dalam Perhitungan
Dalam rumus luas permukaan kubus, panjang sisi (s) menjadi variabel utama. Untuk menentukan luas permukaan kubus, kita perlu mengetahui panjang sisinya terlebih dahulu.
-
Contoh Aplikasi
Misalnya, jika kita ingin menghitung luas permukaan sebuah kubus dengan sisi 5 cm, maka luas permukaan kubus tersebut adalah 6 x (5 cm)2 = 150 cm2.
Dengan demikian, sisi kubus merupakan komponen penting dalam rumus luas permukaan kubus. Pemahaman yang baik tentang konsep sisi kubus sangat penting untuk dapat menggunakan rumus tersebut secara efektif dan akurat.
Persegi
Dalam rumus luas permukaan kubus, konsep persegi memiliki peran penting karena setiap sisi kubus berbentuk persegi. Persegi adalah bangun datar dua dimensi yang memiliki sifat-sifat khusus, yaitu:
-
Empat Sisi Sama Panjang
Sesuai dengan namanya, persegi memiliki empat sisi yang sama panjang. Sifat ini menentukan bentuk persegi yang khas dan menjadi pembeda utama dari bangun datar lainnya.
-
Sudut Siku-siku
Keempat sudut pada persegi siku-siku, artinya masing-masing sudut berukuran 90 derajat. Sudut siku-siku ini membentuk struktur persegi yang stabil dan kokoh.
-
Diagonal Membagi Dua Sisi yang Berhadapan
Dua diagonal yang ditarik pada persegi akan saling berpotongan di titik tengah dan membagi dua sisi yang berhadapan menjadi sama panjang.
-
Luas Persegi
Luas persegi dihitung dengan mengalikan panjang sisinya dengan dirinya sendiri, atau L = s x s, di mana L adalah luas persegi dan s adalah panjang sisi persegi.
Dalam konteks rumus luas permukaan kubus, luas setiap sisi kubus yang berbentuk persegi dihitung menggunakan rumus L = s x s, di mana s adalah panjang sisi kubus. Keenam sisi kubus kemudian dijumlahkan untuk mendapatkan luas permukaan kubus secara keseluruhan, yaitu L = 6 x s2.
Panjang Sisi
Dalam rumus luas permukaan kubus, panjang sisi memegang peranan penting sebagai faktor penentu. Panjang sisi merupakan jarak antara dua titik sudut pada sebuah sisi kubus, dan secara langsung memengaruhi besarnya luas permukaan kubus.
Hubungan antara panjang sisi dan luas permukaan kubus dapat dilihat pada rumus L = 6 x s2. Dalam rumus ini, L adalah luas permukaan kubus, dan s adalah panjang sisi kubus. Dari rumus tersebut, terlihat jelas bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang sisinya. Artinya, jika panjang sisi kubus diperbesar dua kali, maka luas permukaan kubus akan menjadi empat kali lebih besar.
Memahami hubungan ini sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam konstruksi, mengetahui panjang sisi kubus sangat penting untuk menghitung kebutuhan material, seperti luas kain yang dibutuhkan untuk menutupi sebuah kubus atau volume beton yang dibutuhkan untuk membangun sebuah kubus. Dalam desain, panjang sisi kubus menjadi faktor penentu estetika dan fungsionalitas suatu objek yang berbentuk kubus.
Enam
Dalam konteks rumus luas permukaan kubus, jumlah sisi kubus yang berjumlah enam memiliki peran yang sangat penting. Keenam sisi tersebut merupakan bidang datar yang membentuk bangun ruang kubus dan menjadi dasar perhitungan luas permukaannya.
-
Komponen Kubus
Keenam sisi kubus merupakan komponen utama yang membentuk bangun ruang kubus. Sisi-sisi tersebut tersusun secara teratur dan saling tegak lurus, membentuk struktur kubus yang kokoh.
-
Luas Setiap Sisi
Luas permukaan setiap sisi kubus dihitung menggunakan rumus luas persegi, yaitu L = s x s, di mana s adalah panjang sisi kubus. Keenam sisi kubus memiliki luas yang sama.
-
Jumlah Luas Sisi
Luas permukaan kubus diperoleh dengan menjumlahkan luas keenam sisinya. Jumlah sisi yang berjumlah enam menjadi faktor pengali dalam rumus luas permukaan kubus, yaitu L = 6 x s2.
-
Aplikasi Praktis
Memahami hubungan antara jumlah sisi kubus dan rumus luas permukaan kubus sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam konstruksi, menghitung luas permukaan kubus diperlukan untuk menentukan kebutuhan material, seperti luas kain penutup atau volume beton yang dibutuhkan.
Dengan demikian, jumlah sisi kubus yang berjumlah enam merupakan aspek penting dalam rumus luas permukaan kubus, yang menentukan cara perhitungan dan memiliki implikasi dalam berbagai bidang aplikasi.
Kali
Dalam rumus luas permukaan kubus, operasi matematika kali memegang peran penting sebagai penghubung antara panjang sisi kubus dan luas permukaannya.
-
Perkalian Panjang Sisi
Operasi kali digunakan untuk mengalikan panjang sisi kubus dengan dirinya sendiri (s x s). Hasil dari perkalian ini menghasilkan luas setiap sisi persegi yang membentuk kubus.
-
Penjumlahan Luas Sisi
Setelah memperoleh luas setiap sisi, operasi kali digunakan kembali untuk mengalikan jumlah sisi kubus (6) dengan luas setiap sisi (s x s). Hasil dari perkalian ini menghasilkan luas permukaan keseluruhan kubus.
-
Pengaruh Panjang Sisi
Operasi kali menunjukkan keterkaitan antara panjang sisi kubus dan luas permukaannya. Semakin besar panjang sisi kubus, semakin besar pula luas permukaannya. Hal ini sesuai dengan rumus L = 6 x s2, di mana L adalah luas permukaan kubus dan s adalah panjang sisi kubus.
-
Aplikasi Praktis
Memahami operasi kali dalam rumus luas permukaan kubus sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam konstruksi, operasi kali digunakan untuk menghitung kebutuhan material, seperti luas kain penutup atau volume beton yang dibutuhkan untuk membangun sebuah kubus.
Dengan demikian, operasi matematika kali memiliki peran krusial dalam rumus luas permukaan kubus, menghubungkan panjang sisi kubus dengan luas permukaannya dan menjadi dasar perhitungan dalam berbagai aplikasi praktis.
Pertanyaan Umum tentang Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus merupakan rumus yang sangat penting dalam berbagai bidang, seperti matematika, teknik, dan desain. Rumus ini digunakan untuk menghitung luas permukaan bangun ruang kubus, yaitu jumlah luas semua sisi permukaan kubus. Berikut adalah beberapa pertanyaan umum yang sering diajukan terkait rumus luas permukaan kubus:
Pertanyaan 1: Bagaimana cara menghitung luas permukaan kubus?
Jawaban: Luas permukaan kubus dihitung dengan menggunakan rumus L = 6 x s2, di mana L adalah luas permukaan kubus dan s adalah panjang sisi kubus.
Pertanyaan 2: Apa saja faktor-faktor yang memengaruhi luas permukaan kubus?
Jawaban: Luas permukaan kubus dipengaruhi oleh panjang sisi kubus. Semakin besar panjang sisi kubus, semakin besar pula luas permukaan kubusnya.
Pertanyaan 3: Selain panjang sisi, apakah ada faktor lain yang memengaruhi luas permukaan kubus?
Jawaban: Tidak ada faktor lain yang memengaruhi luas permukaan kubus selain panjang sisi kubus.
Pertanyaan 4: Di bidang apa saja rumus luas permukaan kubus digunakan?
Jawaban: Rumus luas permukaan kubus digunakan dalam berbagai bidang, seperti matematika, teknik, dan desain. Dalam matematika, rumus ini digunakan untuk menghitung volume dan luas permukaan bangun ruang lainnya yang berhubungan dengan kubus. Dalam teknik, rumus ini digunakan untuk menghitung kebutuhan material, seperti cat atau ubin, yang diperlukan untuk menutupi permukaan kubus. Dalam desain, rumus ini digunakan untuk menentukan ukuran dan proporsi objek yang berbentuk kubus.
Dengan memahami rumus luas permukaan kubus dan faktor-faktor yang memengaruhinya, kita dapat menyelesaikan berbagai masalah yang berkaitan dengan kubus dengan lebih mudah dan akurat.
Tips untuk Menggunakan Rumus Luas Permukaan Kubus:
- Pastikan untuk mengetahui panjang sisi kubus dengan benar.
- Gunakan rumus L = 6 x s2 dengan tepat.
- Perhatikan satuan panjang yang digunakan (cm, m, atau lainnya).
- Jika diperlukan, konversikan satuan panjang ke satuan yang sama sebelum melakukan perhitungan.
Tips Menggunakan Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus sangat mudah digunakan jika kita memahami konsep dasarnya dengan baik. Berikut adalah beberapa tips yang dapat membantu Anda menggunakan rumus luas permukaan kubus dengan lebih efektif:
Tips 1: Pastikan Anda Mengetahui Panjang Sisi Kubus
Langkah pertama untuk menggunakan rumus luas permukaan kubus adalah memastikan Anda mengetahui panjang sisi kubus. Panjang sisi kubus adalah jarak antara dua titik sudut pada sebuah sisi kubus. Satuan panjang yang digunakan harus konsisten, baik sentimeter (cm), meter (m), atau satuan lainnya.
Tips 2: Gunakan Rumus L = 6 x s2 dengan Tepat
Setelah mengetahui panjang sisi kubus, Anda dapat menggunakan rumus L = 6 x s2 untuk menghitung luas permukaan kubus. Dalam rumus ini, L adalah luas permukaan kubus dan s adalah panjang sisi kubus. Pastikan untuk mengkuadratkan panjang sisi sebelum mengalikannya dengan 6.
Tips 3: Perhatikan Satuan Panjang
Pastikan untuk memperhatikan satuan panjang yang digunakan dalam perhitungan Anda. Jika panjang sisi kubus diberikan dalam sentimeter, maka luas permukaan kubus yang dihasilkan juga akan dalam sentimeter persegi. Jika Anda perlu mengonversi satuan panjang, lakukan konversi sebelum melakukan perhitungan.
Tips 4: Periksa Kembali Hasil Anda
Setelah menghitung luas permukaan kubus, periksa kembali hasil Anda untuk memastikan tidak ada kesalahan. Anda dapat melakukan ini dengan membandingkan hasil Anda dengan nilai yang diketahui atau dengan menggunakan metode lain untuk menghitung luas permukaan kubus.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus luas permukaan kubus dengan lebih percaya diri dan akurat.
Kesimpulan
Rumus luas permukaan kubus adalah alat yang sangat berguna untuk menghitung luas permukaan bangun ruang kubus. Dengan memahami konsep dasar dan tips yang telah dijelaskan di atas, Anda dapat menggunakan rumus ini dengan mudah dan efektif untuk menyelesaikan berbagai masalah yang berkaitan dengan kubus.
KesimpulanRumus luas permukaan kubus merupakan rumus yang penting dan banyak digunakan dalam berbagai bidang, seperti matematika, teknik, dan desain. Rumus ini digunakan untuk menghitung luas permukaan bangun ruang kubus, yaitu jumlah luas semua sisi permukaan kubus.Dengan memahami konsep dasar rumus luas permukaan kubus dan faktor-faktor yang memengaruhinya, kita dapat menyelesaikan berbagai masalah yang berkaitan dengan kubus dengan lebih mudah dan akurat. Rumus ini menjadi dasar perhitungan dalam berbagai aplikasi praktis, seperti menentukan kebutuhan material untuk konstruksi atau menentukan ukuran dan proporsi objek yang berbentuk kubus.Dengan mempelajari dan memahami rumus luas permukaan kubus, kita dapat meningkatkan kemampuan berpikir kritis dan keterampilan problem solving kita. Kita juga dapat mengaplikasikan pengetahuan ini dalam kehidupan sehari-hari, seperti saat kita merencanakan sebuah proyek konstruksi atau mendesain sebuah objek tiga dimensi.




