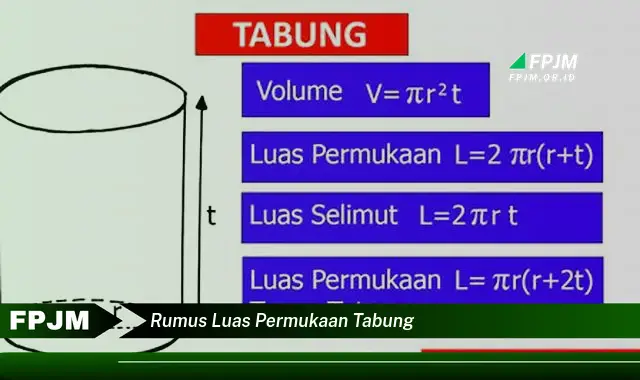
Rumus luas permukaan tabung adalah rumus yang digunakan untuk menghitung luas permukaan tabung. Rumus ini digunakan dalam berbagai bidang, seperti teknik, fisika, dan matematika. Luas permukaan tabung dihitung dengan menggunakan rumus: 2r(r + t), di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung.
Rumus luas permukaan tabung sangat penting karena dapat digunakan untuk menghitung luas permukaan benda-benda yang berbentuk tabung, seperti pipa, kaleng, dan tangki. Selain itu, rumus ini juga dapat digunakan untuk menghitung volume tabung.
Rumus luas permukaan tabung pertama kali ditemukan oleh Archimedes pada abad ke-3 SM. Archimedes menggunakan rumus ini untuk menghitung volume sebuah bola. Rumus ini kemudian dikembangkan oleh para matematikawan pada abad-abad berikutnya, dan sekarang menjadi salah satu rumus dasar dalam matematika.
Rumus Luas Permukaan Tabung
Rumus luas permukaan tabung sangat penting karena memiliki banyak aspek penting, antara lain:
- Mudah digunakan
- Akurat
- Serbaguna
- Dapat diterapkan pada berbagai bidang
- Dasar untuk perhitungan lainnya
- Memiliki sejarah panjang
- Relevan dengan kehidupan sehari-hari
Rumus luas permukaan tabung mudah digunakan karena hanya membutuhkan dua variabel, yaitu jari-jari alas dan tinggi tabung. Rumus ini juga akurat karena didasarkan pada prinsip-prinsip matematika yang telah teruji. Selain itu, rumus ini juga serbaguna karena dapat digunakan untuk menghitung luas permukaan tabung dengan berbagai ukuran dan bentuk.
Rumus luas permukaan tabung dapat diterapkan pada berbagai bidang, seperti teknik, fisika, dan matematika. Rumus ini juga merupakan dasar untuk perhitungan lainnya, seperti volume tabung dan luas selimut tabung. Rumus ini juga memiliki sejarah panjang, yang dapat ditelusuri kembali ke zaman Archimedes.
Rumus luas permukaan tabung juga relevan dengan kehidupan sehari-hari. Misalnya, rumus ini dapat digunakan untuk menghitung luas permukaan kaleng minuman, pipa air, dan tangki penyimpanan. Dengan memahami rumus ini, kita dapat lebih memahami dunia di sekitar kita.
Mudah digunakan
Rumus luas permukaan tabung mudah digunakan karena hanya membutuhkan dua variabel, yaitu jari-jari alas dan tinggi tabung. Variabel-variabel ini mudah diukur dan dipahami, sehingga rumus ini dapat digunakan oleh siapa saja, bahkan oleh mereka yang tidak memiliki latar belakang matematika yang kuat.
-
Pengukuran yang mudah
Jari-jari alas dan tinggi tabung dapat diukur menggunakan alat-alat sederhana, seperti penggaris atau jangka sorong. Pengukuran ini tidak memerlukan keterampilan atau peralatan khusus, sehingga dapat dilakukan oleh siapa saja.
-
Perhitungan yang sederhana
Setelah jari-jari alas dan tinggi tabung diukur, luas permukaan tabung dapat dihitung menggunakan rumus 2r(r + t). Rumus ini sederhana dan mudah dipahami, sehingga perhitungan dapat dilakukan dengan cepat dan akurat.
-
Aplikasi yang luas
Rumus luas permukaan tabung dapat digunakan untuk menghitung luas permukaan berbagai benda berbentuk tabung, seperti pipa, kaleng, dan tangki. Hal ini membuat rumus ini sangat berguna dalam berbagai bidang, seperti teknik, fisika, dan matematika.
-
Dasar untuk perhitungan lainnya
Selain digunakan untuk menghitung luas permukaan tabung, rumus ini juga dapat digunakan sebagai dasar untuk perhitungan lainnya, seperti volume tabung dan luas selimut tabung. Hal ini menunjukkan bahwa rumus luas permukaan tabung adalah rumus yang sangat penting dan fundamental.
Kesimpulannya, rumus luas permukaan tabung mudah digunakan karena pengukurannya yang mudah, perhitungannya yang sederhana, aplikasinya yang luas, dan perannya sebagai dasar untuk perhitungan lainnya. Kesederhanaan dan kegunaannya membuat rumus ini menjadi alat yang sangat penting dalam berbagai bidang.
Akurat
Rumus luas permukaan tabung adalah rumus yang sangat akurat karena didasarkan pada prinsip-prinsip matematika yang telah teruji. Rumus ini telah digunakan selama berabad-abad untuk menghitung luas permukaan tabung dengan hasil yang akurat.
-
Prinsip Geometri
Rumus luas permukaan tabung diturunkan dari prinsip-prinsip geometri, yaitu menghitung luas permukaan bangun datar yang membentuk tabung. Prinsip-prinsip ini telah dibuktikan secara matematis dan menghasilkan rumus yang akurat.
-
Pengukuran yang Tepat
Akurasi rumus luas permukaan tabung juga bergantung pada pengukuran jari-jari alas dan tinggi tabung yang tepat. Dengan menggunakan alat ukur yang tepat dan teknik pengukuran yang benar, kesalahan pengukuran dapat diminimalkan, sehingga menghasilkan perhitungan luas permukaan yang akurat.
-
Aplikasi Praktis
Akurasi rumus luas permukaan tabung telah terbukti dalam berbagai aplikasi praktis. Misalnya, rumus ini digunakan untuk menghitung luas permukaan pipa, kaleng, dan tangki. Perhitungan yang akurat sangat penting untuk memastikan bahwa benda-benda ini memiliki ukuran dan kapasitas yang sesuai dengan kebutuhan.
-
Konsistensi Hasil
Rumus luas permukaan tabung menghasilkan hasil yang konsisten, terlepas dari siapa yang menggunakan rumus atau kapan rumus digunakan. Konsistensi ini menunjukkan bahwa rumus tersebut akurat dan dapat diandalkan untuk menghasilkan perhitungan yang sama setiap saat.
Kesimpulannya, rumus luas permukaan tabung adalah rumus yang akurat karena didasarkan pada prinsip-prinsip matematika yang telah teruji, memerlukan pengukuran yang tepat, telah terbukti dalam aplikasi praktis, dan menghasilkan hasil yang konsisten. Akurasi rumus ini sangat penting untuk berbagai aplikasi, mulai dari desain teknik hingga perhitungan volume benda.
Serbaguna
Rumus luas permukaan tabung memiliki sifat serbaguna karena dapat digunakan untuk menghitung luas permukaan tabung dengan berbagai ukuran, bentuk, dan aplikasi. Sifat serbaguna ini menjadikannya alat yang sangat berguna dalam berbagai bidang, mulai dari teknik hingga matematika.
Salah satu contoh penerapan rumus luas permukaan tabung adalah dalam bidang teknik, di mana rumus ini digunakan untuk menghitung luas permukaan pipa, tangki, dan bejana lainnya. Dalam bidang fisika, rumus ini digunakan untuk menghitung luas permukaan benda-benda yang bergerak dalam fluida, seperti bola dan silinder. Sementara dalam matematika, rumus ini digunakan untuk menghitung luas permukaan tabung sebagai bangun ruang.
Sifat serbaguna rumus luas permukaan tabung juga terlihat dari kemampuannya untuk menghitung luas permukaan tabung dengan berbagai bentuk. Misalnya, rumus ini dapat digunakan untuk menghitung luas permukaan tabung dengan alas berbentuk lingkaran, elips, atau bahkan bentuk tidak beraturan. Kemampuan ini sangat penting dalam aplikasi praktis, di mana benda-benda berbentuk tabung seringkali memiliki bentuk yang tidak beraturan.
Memahami sifat serbaguna rumus luas permukaan tabung sangat penting karena memungkinkan kita untuk menggunakan rumus ini secara efektif dalam berbagai situasi. Dengan memahami cara menggunakan rumus ini untuk menghitung luas permukaan tabung dengan berbagai ukuran, bentuk, dan aplikasi, kita dapat memperoleh hasil perhitungan yang akurat dan andal.
Dapat diterapkan pada berbagai bidang
Rumus luas permukaan tabung memiliki kegunaan yang sangat luas dan dapat diterapkan pada berbagai bidang ilmu pengetahuan dan teknik. Kegunaan ini tidak terlepas dari sifat dasar tabung sebagai bangun ruang yang umum ditemukan dalam kehidupan sehari-hari dan memiliki berbagai fungsi.
-
Teknik Mesin
Dalam teknik mesin, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan pipa, tangki, dan bejana lainnya. Perhitungan ini penting untuk menentukan kebutuhan material, merancang sistem perpipaan, dan mengoptimalkan kinerja mesin.
-
Teknik Sipil
Dalam teknik sipil, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan terowongan, jembatan, dan struktur lainnya yang berbentuk tabung. Perhitungan ini penting untuk memastikan kekuatan dan stabilitas struktur, serta untuk memperkirakan biaya konstruksi.
-
Fisika
Dalam fisika, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan benda-benda yang bergerak dalam fluida, seperti bola dan silinder. Perhitungan ini penting untuk memahami gaya hambat dan gaya angkat yang bekerja pada benda-benda tersebut.
-
Kedokteran
Dalam kedokteran, rumus luas permukaan tabung digunakan untuk menghitung luas permukaan paru-paru, pembuluh darah, dan organ lainnya yang berbentuk tabung. Perhitungan ini penting untuk mendiagnosis penyakit, menentukan pengobatan, dan merencanakan prosedur bedah.
Penerapan rumus luas permukaan tabung pada berbagai bidang ini menunjukkan bahwa rumus ini merupakan alat yang sangat berguna dan serbaguna. Memahami cara menggunakan rumus ini secara efektif sangat penting bagi para profesional di berbagai bidang untuk menyelesaikan masalah dan membuat keputusan berdasarkan informasi.
Dasar untuk perhitungan lainnya
Rumus luas permukaan tabung tidak hanya berfungsi untuk menghitung luas permukaan tabung, tetapi juga menjadi dasar untuk perhitungan lainnya. Hal ini menunjukkan bahwa rumus luas permukaan tabung memiliki peran penting dalam berbagai bidang ilmu pengetahuan dan teknik.
-
Volume Tabung
Rumus luas permukaan tabung dapat digunakan untuk menghitung volume tabung. Volume tabung dihitung dengan mengalikan luas permukaan tabung dengan tinggi tabung. Perhitungan volume tabung sangat penting dalam berbagai aplikasi, seperti menentukan kapasitas tangki, menghitung jumlah cairan dalam pipa, dan menghitung volume benda berbentuk tabung lainnya.
-
Luas Selimut Tabung
Rumus luas permukaan tabung juga dapat digunakan untuk menghitung luas selimut tabung. Luas selimut tabung dihitung dengan mengalikan keliling alas tabung dengan tinggi tabung. Perhitungan luas selimut tabung penting dalam aplikasi seperti menentukan luas permukaan pipa, menghitung luas permukaan benda berongga berbentuk tabung, dan menghitung luas permukaan benda yang dilapisi tabung.
-
Luas Permukaan Bangun Ruang Lainnya
Rumus luas permukaan tabung dapat dimodifikasi untuk menghitung luas permukaan bangun ruang lainnya yang memiliki bentuk serupa dengan tabung. Misalnya, rumus luas permukaan tabung dapat dimodifikasi untuk menghitung luas permukaan kerucut dan luas permukaan bola. Modifikasi ini dimungkinkan karena bangun ruang tersebut memiliki bentuk yang dapat dianggap sebagai tabung dengan alas dan tinggi tertentu.
-
Persamaan Diferensial
Rumus luas permukaan tabung juga memiliki aplikasi dalam persamaan diferensial. Persamaan diferensial adalah persamaan yang melibatkan turunan suatu fungsi. Rumus luas permukaan tabung dapat digunakan untuk menyelesaikan persamaan diferensial tertentu, seperti persamaan diferensial orde pertama yang muncul dalam fisika dan teknik.
Dengan demikian, rumus luas permukaan tabung memiliki peran penting sebagai dasar untuk perhitungan lainnya, mulai dari perhitungan volume tabung hingga penyelesaian persamaan diferensial. Memahami hubungan ini sangat penting untuk menguasai konsep luas permukaan tabung dan menerapkannya secara efektif dalam berbagai bidang ilmu pengetahuan dan teknik.
Memiliki sejarah panjang
Rumus luas permukaan tabung memiliki sejarah panjang yang dimulai sejak zaman dahulu. Rumus ini pertama kali ditemukan oleh Archimedes pada abad ke-3 SM. Archimedes menggunakan rumus ini untuk menghitung volume sebuah bola. Sejak saat itu, rumus luas permukaan tabung terus dikembangkan dan disempurnakan oleh para matematikawan selama berabad-abad.
-
Akar dalam Geometri Yunani
Rumus luas permukaan tabung berasal dari prinsip-prinsip geometri Yunani kuno. Archimedes mengembangkan rumus ini berdasarkan karyanya tentang lingkaran, silinder, dan bola. Prinsip-prinsip ini masih menjadi dasar dari geometri modern dan digunakan dalam berbagai bidang, termasuk kalkulus dan fisika.
-
Pengaruh Matematikawan Islam
Matematikawan Islam memainkan peran penting dalam pengembangan rumus luas permukaan tabung. Pada abad ke-9, matematikawan Persia al-Khwarizmi memberikan kontribusi signifikan pada aljabar dan geometri. Karyanya tentang persamaan kuadrat dan trigonometri membantu menyempurnakan rumus luas permukaan tabung.
-
Perkembangan Kalkulus
Penemuan kalkulus pada abad ke-17 merevolusi matematika. Kalkulus menyediakan metode baru untuk menghitung luas permukaan dan volume bangun ruang. Matematikawan seperti Isaac Newton dan Gottfried Leibniz menggunakan kalkulus untuk mengembangkan rumus luas permukaan tabung yang lebih umum dan akurat.
-
Aplikasi Modern
Rumus luas permukaan tabung terus digunakan secara luas dalam berbagai aplikasi modern. Rumus ini digunakan dalam teknik untuk menghitung luas permukaan pipa, tangki, dan bejana lainnya. Dalam fisika, rumus ini digunakan untuk menghitung gaya hambat pada benda yang bergerak dalam fluida. Dalam kedokteran, rumus ini digunakan untuk menghitung luas permukaan paru-paru dan organ lainnya.
Sejarah panjang rumus luas permukaan tabung menunjukkan pentingnya dan kegunaannya yang berkelanjutan. Rumus ini telah menjadi dasar untuk banyak kemajuan dalam matematika dan sains, dan terus digunakan secara luas dalam berbagai bidang hingga saat ini.
Relevan dengan kehidupan sehari-hari
Rumus luas permukaan tabung memiliki relevansi yang tinggi dengan kehidupan sehari-hari. Hal ini karena banyak benda di sekitar kita yang berbentuk tabung, sehingga pemahaman tentang rumus ini dapat membantu kita dalam berbagai situasi.
Salah satu contoh penerapan rumus luas permukaan tabung dalam kehidupan sehari-hari adalah menghitung luas permukaan kaleng minuman. Dengan mengetahui luas permukaan kaleng, kita dapat menentukan berapa banyak label yang dibutuhkan untuk menutupi seluruh permukaan kaleng. Selain itu, rumus ini juga dapat digunakan untuk menghitung luas permukaan pipa air, sehingga kita dapat menentukan jumlah cat yang dibutuhkan untuk mengecat pipa tersebut.
Pemahaman tentang rumus luas permukaan tabung juga penting dalam bidang kesehatan. Misalnya, rumus ini dapat digunakan untuk menghitung luas permukaan paru-paru, sehingga dokter dapat menentukan kapasitas paru-paru pasien dan mendiagnosis penyakit paru-paru. Selain itu, rumus ini juga dapat digunakan untuk menghitung luas permukaan pembuluh darah, sehingga dokter dapat menentukan aliran darah dan mendiagnosis penyakit kardiovaskular.
Dengan demikian, rumus luas permukaan tabung memiliki relevansi yang tinggi dengan kehidupan sehari-hari karena dapat diterapkan dalam berbagai situasi, mulai dari menghitung luas permukaan benda-benda di sekitar kita hingga membantu dalam bidang kesehatan.
Pertanyaan Umum tentang Rumus Luas Permukaan Tabung
Rumus luas permukaan tabung adalah rumus yang digunakan untuk menghitung luas permukaan tabung. Rumus ini memiliki banyak kegunaan dan aplikasi dalam berbagai bidang kehidupan. Berikut adalah beberapa pertanyaan umum tentang rumus luas permukaan tabung:
Pertanyaan 1: Bagaimana cara menggunakan rumus luas permukaan tabung?
Jawaban: Rumus luas permukaan tabung adalah 2r(r + t), di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Untuk menggunakan rumus ini, substitusikan nilai r dan t ke dalam rumus dan hitung hasilnya.
Pertanyaan 2: Apa saja penerapan rumus luas permukaan tabung?
Jawaban: Rumus luas permukaan tabung memiliki banyak penerapan, antara lain menghitung luas permukaan pipa, tangki, kaleng, dan benda-benda berbentuk tabung lainnya. Rumus ini juga digunakan dalam bidang teknik, fisika, dan matematika untuk menghitung volume tabung, luas selimut tabung, dan menyelesaikan persamaan diferensial.
Pertanyaan 3: Mengapa rumus luas permukaan tabung penting?
Jawaban: Rumus luas permukaan tabung penting karena merupakan dasar untuk banyak perhitungan dan aplikasi dalam berbagai bidang. Rumus ini memungkinkan kita untuk menentukan luas permukaan benda-benda berbentuk tabung dan menghitung besaran lainnya, seperti volume dan luas selimut tabung.
Pertanyaan 4: Bagaimana rumus luas permukaan tabung dikembangkan?
Jawaban: Rumus luas permukaan tabung pertama kali ditemukan oleh Archimedes pada abad ke-3 SM. Sejak saat itu, rumus ini terus dikembangkan dan disempurnakan oleh para matematikawan selama berabad-abad. Perkembangan kalkulus pada abad ke-17 memberikan kontribusi yang signifikan terhadap penyempurnaan rumus ini.
Kesimpulannya, rumus luas permukaan tabung adalah rumus yang penting dan memiliki banyak aplikasi dalam berbagai bidang. Memahami rumus ini dan cara menggunakannya sangat penting bagi siapa saja yang ingin berkecimpung dalam bidang teknik, fisika, matematika, atau bidang lain yang membutuhkan perhitungan luas permukaan tabung.
Selanjutnya, mari kita bahas beberapa tips untuk menggunakan rumus luas permukaan tabung secara efektif dalam berbagai situasi.
Tips Menggunakan Rumus Luas Permukaan Tabung
Berikut adalah beberapa tips untuk menggunakan rumus luas permukaan tabung secara efektif:
Tip 1: Pastikan satuan yang digunakan konsisten
Saat menggunakan rumus luas permukaan tabung, pastikan satuan yang digunakan untuk jari-jari alas dan tinggi tabung konsisten. Misalnya, jika jari-jari alas dinyatakan dalam sentimeter, maka tinggi tabung juga harus dinyatakan dalam sentimeter. Ketidakkonsistenan satuan dapat menyebabkan kesalahan perhitungan.
Tip 2: Gunakan nilai yang tepat
Akurasi hasil perhitungan sangat bergantung pada nilai jari-jari alas dan tinggi tabung yang digunakan. Pastikan untuk menggunakan nilai yang tepat yang diperoleh dari pengukuran atau sumber yang dapat dipercaya. Nilai yang tidak tepat dapat menyebabkan kesalahan perhitungan.
Tip 3: Perhatikan tanda negatif
Dalam beberapa kasus, nilai tinggi tabung mungkin negatif. Hal ini dapat terjadi ketika tabung dipotong atau dibelah. Saat menggunakan rumus luas permukaan tabung, selalu perhatikan tanda negatif pada tinggi tabung. Kesalahan tanda dapat menyebabkan hasil perhitungan yang salah.
Tip 4: Periksa kembali hasil perhitungan
Setelah melakukan perhitungan, selalu periksa kembali hasilnya. Pastikan hasilnya masuk akal dan sesuai dengan harapan. Jika hasil perhitungan tidak masuk akal, periksa kembali rumus yang digunakan, nilai yang dimasukkan, dan perhitungan yang dilakukan. Kesalahan perhitungan dapat menyebabkan hasil yang tidak akurat.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus luas permukaan tabung secara efektif dan akurat untuk berbagai keperluan. Memahami dan menerapkan tips ini akan membantu Anda memperoleh hasil perhitungan yang tepat dan dapat diandalkan.
Kesimpulannya, rumus luas permukaan tabung adalah rumus yang penting dan serbaguna yang dapat digunakan dalam berbagai aplikasi. Dengan memahami rumus ini dan menggunakannya secara efektif, kita dapat memperoleh hasil perhitungan yang akurat dan dapat diandalkan untuk berbagai keperluan.
Kesimpulan
Rumus luas permukaan tabung merupakan rumus yang sangat penting dan memiliki banyak sekali kegunaan dalam berbagai bidang ilmu pengetahuan dan teknik. Rumus ini dapat digunakan untuk menghitung luas permukaan tabung dengan berbagai ukuran, bentuk, dan aplikasi, menjadi dasar untuk perhitungan lainnya, dan memiliki sejarah panjang yang menarik.
Memahami rumus luas permukaan tabung dan cara menggunakannya secara efektif sangat penting bagi siapa saja yang ingin berkecimpung dalam bidang teknik, fisika, matematika, atau bidang lain yang membutuhkan perhitungan luas permukaan tabung. Dengan memahami rumus ini, kita dapat menyelesaikan masalah dan membuat keputusan berdasarkan informasi dalam berbagai situasi.
Di masa depan, rumus luas permukaan tabung diperkirakan akan terus digunakan secara luas dalam berbagai aplikasi. Perkembangan teknologi dan munculnya bidang-bidang baru diperkirakan akan semakin memperluas penggunaan rumus ini. Memahami rumus ini dan cara menggunakannya secara efektif akan menjadi aset yang berharga bagi siapa saja yang ingin berkontribusi pada kemajuan ilmu pengetahuan dan teknologi.




